Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 105
Em uma operação de extração de madeira, a tora de madeira flutua rio abaixo em direção a uma serraria. É um ano seco e o leito do rio está tão baixo que, em alguns locais, a profundidade é de . Qual é o maior diâmetro de tora que pode ser transportado
dessa forma (partindo de uma distância mínima de entre a tora e o fundo do rio e considerando que a madeira tem )?
Passo 1
Nesse problema temos uma situação em um rio, onde devemos encontrar o maior diâmetro de tora que será transportado.
Utilizamos as seguintes equações:
, força de empuxo
, somatório de forças no sentido de
Passo 2
Pelo diagrama de corpo livre, temos a seguinte analise de forças:
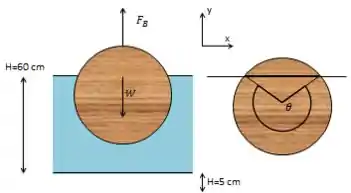
Onde:
Em alguns problemas pode ser pedido a área da parte submersa, portanto, para isso podemos encontrar em livros a seguinte relação:
onde é o raio e é o ângulo incluído.
Portanto, obtemos
Eliminando termos semelhantes,
Usando uma calculadora, temos que
Da geometria, a quantidade submersa de uma tora é e também . Relacionando as duas equações:
Isolando o ,
Como o diâmetro é , temos