Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 5.Problemas - Ex. 35

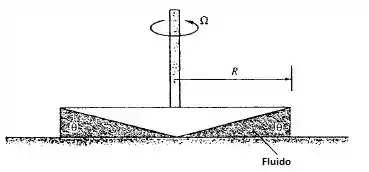
O torque M requerido para acionar o viscosímetro do tipo cone-placa (mostrado abaixo) depende do raio R, da velocidade de rotação Ω , da viscosidade do fluido μ e do ângulo θ do cone. Reescreva essa relação em forma adimensional. Como a relação se simplifica se soubermos que M é proporcional a θ ?

Passo 1

Vamos para mais um desafio da mecânica dos fluidos combinando a análise adimensional rsrs?

Vamos escrever matematicamente como as coisas são função de outras?

M = f ( R ,   Ω ,   μ ,   θ )

Quais são as unidades bases desses parâmetros?

M = M L 2 T - 2

R = L

Ω = T - 1

μ = M L - 1 T - 1

θ = 1

Como temos 5 variáveis (n), e temos 3 dimensões bases (MLT), tem-se que o número de grupos pi iguais a 5 – 3 = 2 grupos!

Sendo que um grupo COM CERTEZA será θ uma vez que ele tem dimensão 1!!!

Passo 2

Bem, podemos então escrever o outro grupo que queremos encontrar, certo?

Π 1 = R a Ω b μ c M

Passo 3

Vamos agora fazer as análises dimensionais e assim montar as equações algébricas!!!

Π 1 = R a Ω b μ c M

L a T - 1 b M L - 1 T - 1 c M L 2 T - 2 = { M 0 L 0 T 0 }

M : c + 1 = 0 → c = - 1

L : a - c + 2 = 0 → a = - 3

T : - b - c - 2 = 0 → b = - 1

Π 1 = M μ Ω R 3

Passo 4

M μ Ω R 3 = f ( θ )

Se temos que M   ∝ θ , temos que:

M μ Ω R 3 θ = c o n s t a n t e

Resposta

M μ Ω R 3 θ = c o n s t a n t e

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Medições da altura de líquido a montante de uma obstrução colocada em um escoamento de canal­ aberto podem ser usadas para determinar a vazão em volume. (Tais obstruções, projetadas e calibradas para
O tempo, t , para drenagem de óleo para fora de um recipiente de calibração de viscosidade depende da viscosidade, μ , e massa específica, ρ , do fluido, do diâmetro do orifício, d , e da aceleração d
Uma correia continua, movendo verticalmente através de um banho de líquido viscoso, arrasta uma camada de líquido de espessura h ao longo dela. Considere que a vazão volumétrica de líquido, Q , depend
No exemplo 5.1 usamos o teorema de pi para desenvolver a equação 5.2 com base na equação 5.1. Em lugar de simplesmente listar as dimensões de cada variável, alguns pesquisadores listam as potências de
A velocidade de propagação C de uma onda capilar em água profunda é conhecida como uma função apenas da massa específica ρ , comprimento de onda λ e da tensão superficial γ . Encontre a relação funcio