Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 77
Um transistor, que pode ser aproximado por uma fonte de calor hemisférica com raio , está inserido em um grande substrato de silício e dissipa calor a uma taxa . Todas as fronteiras do silício são mantidas à temperatura ambiente de , exceto a superfície superior, que se encontra isolada termicamente.
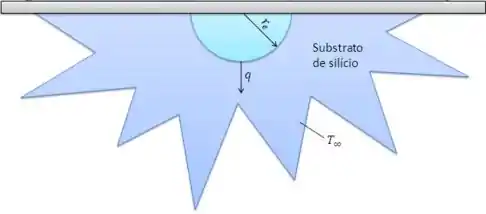
Obtenha uma expressão geral para a distribuição de temperaturas no substrato e determine a temperatura da superfície da fonte de calor para .
Passo 1
Temos um transistor semi-esférico com uma temperatura de superfície e que dissipa para o substrato de silício. Devemos obter o perfil de temperaturas no substrato e, a temperatura . Vamos lá???
Vamos começar adotando alguns pontos. O processo de transferência de calor ocorre em regime permanente e apenas na direção radial. Então, a taxa de transferência de calor através do transistor é constante. No interior do substrato a transferência de calor se dá apenas por condução. Aplicando a lei de Fourier:
Como só temos constantes do lado esquerdo:
Integrando:
Passo 2
Para encontrar as constantes e vamos aplicar as condições de contorno do sistema. Sabemos que para uma distância muito grande a temperatura da fronteira do substrato é . Então:
A outra condição é que em a temperatura é :
E o perfil de temperatura fica:
Passo 3
Vamos agora determinar a temperatura da superfície para o caso em que . Pela lei de Fourier:
Para :
Resposta
Perfil de temperatura:
E .