Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 12.Problemas - Ex. 55

A variação da absortividade espectral de uma superfície é dada na figura a seguir. Determine a absortividade e a refletividade média da superfície para uma radiação originária de uma fonte a T = 2.500 K. Além disso, determine a emissividade média dessa superfície a 3.000 K.

Passo 1

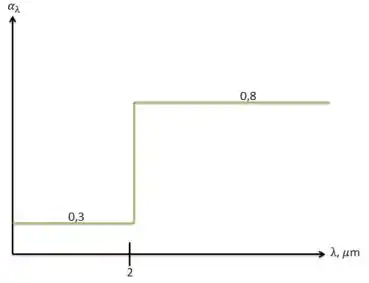
Temos uma superfície com perfil de absortividade

α λ = α 1 = 0 , 3 ,           0 ≤ λ < 2   μ m α 2 = 0 , 8 ,         2   μ m ≤ λ < ∞

A partir deste perfil devemos calcular a absortividade e refletividade média da superfície para uma temperatura T = 2.500   K . Após isso, ainda devemos encontrar a emissividade média do material para T = 3.000   K . Vamos lá?

Passo 2

Vamos começar calculando a absortividade média a partir do perfil. A absortividade média pode ser calculada por:

α T = ∫ 0 ∞ α λ λ , T E b λ λ , T d λ σ T 4

α T = ∫ 0 2   μ m α λ λ , T E b λ λ , T d λ + ∫ 2   μ m ∞ α λ λ , T E b λ λ , T d λ σ T 4

α T = ∫ 0 2   μ m 0,3 x E b λ λ , T d λ + ∫ 2   μ m ∞ 0 , 8 x E b λ λ , T d λ σ T 4

α T = 0,3 x ∫ 0 2   μ m E b λ λ , T d λ + 0,8 x ∫ 2   μ m ∞ E b λ λ , T d λ σ T 4

α T = 0,3 x ∫ 0 2   μ m E b λ λ , T d λ + 0 , 8 x ( ∫ 0 ∞ E b λ λ , T d λ - ∫ 0 2   μ m E b λ λ , T d λ ) σ T 4

Podemos aproximar ∫ 0 λ E λ , b d λ utilizando a função de radiação f λ :

∫ 0 λ E λ , b d λ = σ T 4 f λ

Vamos usar isso para encontrar a emissividade hemisférica total:

α T = 0,3 x ∫ 0 2   μ m E b λ λ , T d λ + 0,8 x ( ∫ 0 ∞ E b λ λ , T d λ - ∫ 0 2   μ m E b λ λ , T d λ ) σ T 4

α T = 0 , 3 x σ T 4 x f 0 - 2   μ m + 0 , 8 x σ T 4 x ( f 0 - ∞ - f 0 - 2   μ m ) σ T 4

α T = 0 , 3 x f 0 - 2   μ m + 0 , 8 x ( f 0 - ∞ - f 0 - 2   μ m )

Pela tabela 12-2 do capítulo do livro temos que para:

∞ x T → f = 1

2   μ m   x   2 . 5 00   K = 5 . 000   μ m . K → f = 0 , 633747

Então, nossa emissividade é:

α T = 0 , 3 x 0 , 633747 + 0 , 8 x ( 1 - 0 , 633747 )

α = 0 , 483

Agora, devemos determinar a refletividade do material. Para qualquer corpo:

α + ρ + τ = 1

Considerando que a superfície é opaca → τ = 0 . Portanto:

α + ρ + 0 = 1

ρ = 1 - α

ρ = 1 - 0 , 483

ρ = 0 , 51 7

Passo 3

Nos resta ainda determinar a emissividade do material em T = 3.000   K . Para isso vamos primeiro usar a lei de Kirchhoff. A lei de Kirchhoff diz que, para uma mesma temperatura, a absortividade espectral é igual à emissividade espectral, ou seja:

α λ = ε λ

Então temos que o perfil de emissividade é:

ε λ = ε 1 = 0,3 ,           0 ≤ λ < 2   μ m ε 2 = 0,8 ,         2   μ m ≤ λ < ∞

Para determinar a emissividade média em 3.000 K iremos usar um procedimento análogo ao que usamos para a absortividade. A emissividade média é calculada por:

ε T = ∫ 0 ∞ ε λ λ , T E b λ λ , T d λ σ T 4

ε T = ∫ 0 2   μ m ε λ λ , T E b λ λ , T d λ + ∫ 2   μ m ∞ ε λ λ , T E b λ λ , T d λ σ T 4

ε T = ∫ 0 2   μ m 0 , 3 x E b λ λ , T d λ + ∫ 2   μ m ∞ 0,8 x E b λ λ , T d λ σ T 4

ε T = 0,3 x ∫ 0 2   μ m E b λ λ , T d λ + 0,8 x ∫ 2   μ m ∞ E b λ λ , T d λ σ T 4

ε T = 0,3 x ∫ 0 2   μ m E b λ λ , T d λ + 0,8 x ( ∫ 0 ∞ E b λ λ , T d λ - ∫ 0 2   μ m E b λ λ , T d λ ) σ T 4

Podemos aproximar ∫ 0 λ E λ , b d λ utilizando a função de radiação f λ :

∫ 0 λ E λ , b d λ = σ T 4 f λ

Vamos usar isso para encontrar a emissividade hemisférica total:

ε T = 0,3 x ∫ 0 2   μ m E b λ λ , T d λ + 0,8 x ( ∫ 0 ∞ E b λ λ , T d λ - ∫ 0 2   μ m E b λ λ , T d λ ) σ T 4

ε T = 0 , 3 x σ T 4 x f 0 - 2   μ m + 0 , 8 x σ T 4 x ( f 0 - ∞ - f 0 - 2   μ m ) σ T 4

ε T = 0,3 x f 0 - 2   μ m + 0,8 x ( f 0 - ∞ - f 0 - 2   μ m )

Pela tabela 12-2 do capítulo do livro temos que para:

∞ x T → f = 1

2   μ m   x   3.000   K = 6 . 000   μ m . K → f = 0 , 737818

Então, nossa emissividade é:

ε T = 0 , 3 x 0 , 737818 + 0 , 8 x ( 1 - 0 , 737818 )

ε = 0 , 431

Resposta

A absortividade e refletividade média da superfície para uma fonte a 2.500 K são α = 0,483 e ρ = 0,517 . Se a superfície estiver a uma temperatura de 3.000 K sua emissividade média será de ε = 0,431 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

56 - A absortividade hemisférica espectral de uma superfície opaca tem o comportamento mostrado a seguir.Qual é a absortividade solar, α S ? Se for considerado que ε λ = α λ e que a superfície se enco
44 - Estime a emissividade hemisférica total ε de aço inoxidável polido a 800K , usando a Equação 12.43 com as informações fornecidas na Figura 12.17. Suponha que a emissividade hemisférica é igual à
51 - A distribuição da refletividade espectral de uma tinta branca (Figura 12.22) pode ser aproximada pela seguinte função degrau:Uma pequena placa plana revestida com essa tinta encontra-se suspensa
46 - Para um comprimento de onda λ especificado, medidas da intensidade espectral I λ , e ( λ ,T )=ε λ I λ , c n da radiação emitida por uma superfície difusa podem ser usadas para determinar a temper
45 - Um termômetro de radiação é um instrumento que responde a um fluxo radiante em um intervalo espectral estabelecido e é calibrado para indicar a temperatura de um corpo negro que produz o mesmo fl