Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 11.Problemas - Ex. 35
Um trocador de calor de tubos geminados, que opera em contracorrente, é construído pela soldagem de dois tubos circulares de níquel, cada um com de comprimento, conforme mostrado na figura. Água quente escoa pelo tubo menor, com de diâmetro, e ar, a pressão atmosférica, escoa através do tubo maior que tem de diâmetro. Os dois tubos têm uma espessura de parede de . A condutância térmica de contato por unidade de comprimento da junta soldada é de . As vazões mássicas da água e do ar são e , respectivamente. As temperaturas de entrada da água e do ar são de e , respectivamente.
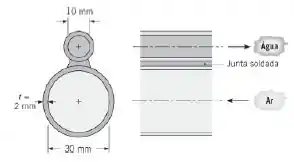
Empregue o método para determinar a temperatura de saída do ar.
Leve em consideração os efeitos da condução circunferencial nas paredes dos tubos tratando-as como se fossem superfícies estendidas.
Passo 1
Começamos o problema supondo temperaturas médias para a água e o ar.
Após, obtemos nas Tabelas do Apêndice A as propriedades para cada fluído.
Na Tabela , para água sob obtemos as seguintes propriedades:
Na Tabela , para o ar sob obtemos:
Na Tabela , para o níquel sob , obtemos:
Passo 2
O número de unidades de transferência para análise do trocador de calor é expresso por:
Já a eficácia do trocador de calor:
Para um trocador de calor em contracorrente, a eficácia é dada como:
A razão da capacidade térmica é dada por:
Calculando a capacidade térmica do fluido quente:
Com:
.
Temos:
Calculando a capacidade térmica do fluido frio:
Com:
.
Temos:
Assim:
Aplicando na razão:
Aplicando na eficácia:
Pelo balanço de energia:
Já a taxa máxima de transferência de calor é:
Assim, reescrevemos a eficácia como:
Com :
Passo 3
Calculando o número de Reynolds para o fluido quente:
Calculando o número de Reynolds para o fluido frio:
Pela equação de Dittus-Boelter para fluxo turbulento totalmente desenvolvido, calculamos o número de Nusselt:
Como:
Então:
Para o fluido quente (:
Para o fluido frio (:
Passo 4
Pela equação 11.1, temos:
Para o fluido quente, a eficácia da temperatura lateral é calculada por:
Onde:
Dados:
.
Temos:
Assim, sendo:
Temos:
Para o fluido frio, a eficácia da temperatura lateral é calculada por:
Onde:
Temos:
Assim, sendo:
Temos:
Passo 5
Calculando e :
Substituindo os dados obtidos na equação do começo do Passo 4, com , obtemos:
Passo 6
No Passo 2, mostramos que:
Assim:
Aplicando na equação obtida no Passo 3, com:
;
.
Temos: