Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 66
Um tubo horizontal transporta fluido em escoamento turbulento completamente desenvolvido. A diferença de pressão estática medida entre duas seções é 35 kPa. A distância entre as seções é 10 m e o diâmetro do tubo é 150 mm. Calcule a tensão de cisalhamento, , que atua sobre as paredes.
Passo 1
Neste problema há um escoamento completamente desenvolvido ao longo de um tubo. O objetivo é obter a tensão de cisalhamento () que atua na parede do tubo.
Para isso será necessário o uso da equação de Balanço de Quantidade de Movimento (relação integral) ao longo de um volume de controle, conforme Figura abaixo.
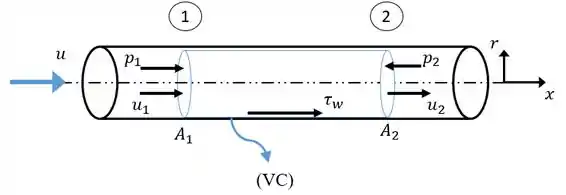
A equação de Balanço de Quantidade de Movimento, aplicada apenas ao longo de x, é definida como:
E será aplicada ao longo das seções 1 e 2, tendo como hipóteses:
- regime permanente ();
- escoamento incompressível ();
- escoamento completamente desenvolvido (
- seção transversal constante (;
- escoamento horizontal (força de campo nula - ).
Passo 2
A partir das hipóteses, a equação de balanço apresentada no Passo 1 pode ser escrita como:
Em função das hipóteses do problema, pode-se afirma que o fluxo de quantidade de movimento nas superfícies e são iguais:
Logo:
Passo 3
Sabendo que a equação de Balanço de Quantidade de Movimento se reduziu a:
E que representam as forças de superfície (força devido à pressão e à tensão de cisalhamento), então ela pode ser escrita como:
Nota: sinal positivo no sentido do eixo x.
Então, isolando o termo :
Logo:
Rearranjando o termo de diferença de pressão para escrever o termo queda de pressão ():
De forma que a tensão de cisalhamento na parede pode ser escrita como:
Passo 4
Utilizando os valores numéricos definidos no enunciado (; e ):
Logo, a tensão de cisalhamento sobre a parede é:
Atenção: o sinal negativo de indica que a tensão de cisalhamento atua no sentido contráro ao escoamento do fluido.