Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 41
Um tubo redondo e poroso, com , transporta água. A velocidade de entrada é uniforme com . A água vaza para fora do tubo através das paredes porosas, radialmente e com simetria em relação ao eixo do tubo. A distribuição de velocidades da água vazando ao longo do tubo é dada por
em que e . Calcule a vazão mássica dentro do tubo em .
Passo 1
Dados fornecidos:
O diâmetro do tubo redondo poroso é .
A velocidade na entrada é .
A velocidade inicial é .
O comprimento é .
Um esboço de um volume de controle pode ser feiro da seguinte maneira:
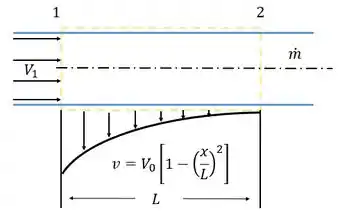
Passo 2
Para encontrar a vazão mássica dentro do tubo, podemos aplicando equação da conservação de massa.
Podemos considerar o caso geral de fluxo constante através de um volume de controle fixo. Por definição, nenhuma propriedade de fluido varia com o tempo em um fluxo constante. Consequentemente, o primeiro termo da equação acima é zero para fluxo constante.
Assim, a declaração de conservação de massa se reduz a:
Passo 3
A relação acima pode ser expressa como:
Passo 4
Para calcular a vazão mássica dentro do tubo em , basta substituirmos os dado fornecidos no enunciado na equação acima. Aqui a densidade da água é .
Agora, substituindo os valores conhecidos na equação, obtemos:
Portanto, a vazão mássica dentro do tubo é .