Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 4

Para o escoamento de óleo SAE 30 por um tubo de 5 cm de diâmetro, Fig. A.1, para qual vazão em m3/h devemos esperar transição para a turbulência a (a) 20 °C e (b) 100°C?

Passo 1

E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!

A primeira ideia que a gente tem que ter da questão é de qual assunto ela faz parte. Esse problema em específico é referente à seção 6.1 do livro, chamada “Regimes de número de Reynolds”.

Nesse problema, temos óleo SAE 30 escoando em um tubo de diâmetro D = 0,05   m a duas temperaturas: 20   ° C e 100   ° C

O enunciado pede pra gente calcular a vazão volumétrica em m 3 / h para um número de Reynolds onde ocorrerá a transição para a turbulência, ou seja, para o caso de um tubo circular, R e d , c r ≈ 2300 .

Pra resolver o problema, vamos antes precisar encontrar os valores de massa específica ρ e viscosidade μ do óleo a 20   ° C e 100   ° C .

Vem comigo pra resolvermos essa questão juntos!

Passo 2

Primeiro, vamos encontrar os valores de massa específica ρ e viscosidade μ para o óleo SAE 30 a 20   ° C . Pra achar esses valores, basta a gente ir na Tabela A.3, intitulada “Propriedades dos líquidos comuns a 1 atm e 20°C”, na página 829.

Os valores encontrados são:

T = 20 ° C →   ρ = 891 k g m 3 μ = 0,29 k g m . s

Como o fluido é um líquido, o valor da massa específica não varia com a temperatura, e será a mesma a 100   °   C .

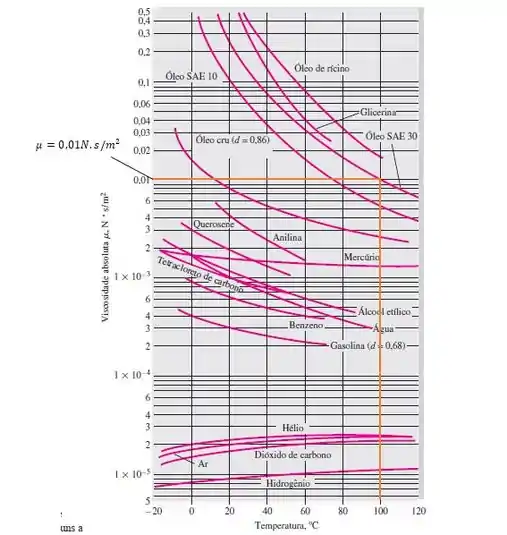
Agora, devemos encontrar a viscosidade a 100 ° C . Pra isso, vamos na Figura A.1, intitulada “Viscosidade absoluta de fluidos comuns a 1 atm”.

Olhe a figura abaixo, veja as linhas laranjas partindo do valor de temperatura que queremos, cruzando a curva correspondente ao Óleo SAE 30, e o valor de viscosidade μ = 0,01   N . s / m ² que encontramos no eixo y.

Passo 3

Pra finalizar a questão, vamos calcular as vazões volumétricas nas duas temperaturas especificadas.

Em primeiro lugar, para a temperatura de 20   ° C :

Q 20 ° c =   μ 20 ° C R e d , c r   A ρ D = 0,29 k g m . s 2300 π 4 ( 0,05   m ) ² 891 k g m 3 0,05   m = 0,029 m 3 s = 105,8 m 3 h

Agora, para a temperatura de 100   ° C :

Q 100 ° c =   μ 20 ° C R e d , c r   A ρ D = 0,01   N . s / m ² 2300 π 4 ( 0,05   m ) ² 891 k g m 3 0,05   m = 0,00101 m 3 s = 3,65 m 3 h

Pronto, matamos a questão juntos!

Resposta

A vazão volumétrica nas condições do escoamento é (a) Q 20 ° c = 105,8 m 3 h a 20 ° C e (b) Q 100 ° c = 3,65 m 3 h a 100   ° C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Água escoa em regime permanente sobre uma placa plana porosa. Uma sucção constante é aplicada ao longo da seção porosa. O perfil de velocidade na seção c d é u U ∞ = 3 y δ - 2 y δ 3 / 2 Avalie a vazão
Um funil cônico, com meio ângulo θ = 15 ° , com diâmetro máximo D = 70m m e altura H , deixa escapar líquido por um orifício (diâmetro d = 3,12m m ) no seu vértice. A velocidade do líquido deixando o
Um tanque cilíndrico de diâmetro D = 50m m , possui o esgoto por uma abertura de diâmetro d = 5m m , em seu fundo. A velocidade do líquido saindo do tanque é aproximadamente V = 2 g h , em que y é a a
Para as condições do Problema 4.48, estime o tempo requerido para drenar o tanque à profundidade de y = 0,3m (uma mudança na profundidade de 0,1m ), e de y = 0,3m para y = 0,2m (também uma mudança na
Em um funil cônico, com meio ângulo θ = 30 ° , o líquido é drenado através de um pequeno orifício de diâmetro d = 6,25m m no vértice do funil. A velocidade do líquido através do orifício é dada, aprox