Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 48
Um tanque cilíndrico de diâmetro , possui o esgoto por uma abertura de diâmetro , em seu fundo. A velocidade do líquido saindo do tanque é aproximadamente , em que é a altura do fundo do tanque à superfície livre. Se o tanque inicialmente está cheio com água a , determine a profundidade da água em , e . Trace o gráfico de em função de para os primeiros segundos.
Passo 1
Nos foi dado no enunciado que:
Podemos fazer as seguintes considerações:
Fluxo uniforme
Fluxo incompressível
Negligenciar a densidade do ar
Passo 2
Feito as considerações, podemos usar e equação da conservação de massa para o volume de controle.
A equação básica se torna
Passo 3
Podemos aqui, fazer as seguintes substituições:
e
Substituindo na equação encontrada no passo 2 temos:
Podemos agora integrar dos dois lados.
Passo 4
Podemos encontrar a função , que determina a profundidade no tanque, substituindo os valores fornecido no enunciado na equação encontrada no passo anterior. Assim temos:
Passo 5
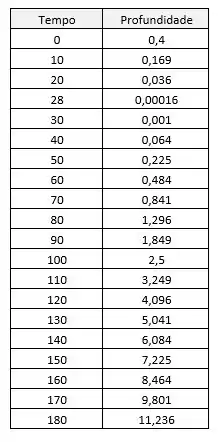
Para calcular da profundidade da água nos tempos desejados, basta usamos a função que encontramos no passo anterior.
Para :
Para :
Para :
Os resultados não fazem sentido, pois a tanque estaria vazio antes dos segundos. Comparando o livro com a versão em inglês, podemos perceber que os dados fornecidos são totalmente diferente e não fazem sentido.
Passo 6
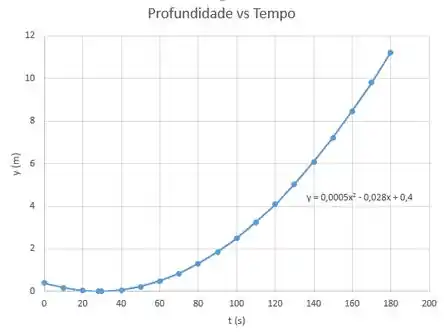
Aqui, temos a tabela e o gráfico da profundidade da água em função do tempo usando o software Microsoft Excel.
