Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 2
Ar a aproximadamente 1 atm escoa por um tubo horizontal de 4 cm de diâmetro. (a) Deduza uma fórmula para Qmáx, a vazão volumétrica máxima para a qual o escoamento permanece laminar, e plote Qmáx em função da temperatura na faixa 0°C
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
A primeira ideia que a gente tem que ter da questão é de qual assunto ela faz parte. Esse problema em específico é referente à seção 6.1 do livro, chamada “Regimes de número de Reynolds”.
Nesse problema, temos ar escoa por um tubo horizontal de diâmetro .
O enunciado nos pede que a gente encontre uma fórmula para a vazão volumétrica máxima para qual o escoamento permanece laminar, ou seja, para quando o número de Reynolds for .
Além disso, devemos plotar um gráfico de em função da temperatura na faixa .
Vem comigo pra gente resolver essa questão juntos!
Passo 2
Em primeiro lugar, devemos lembrar qual a equação utilizada para calcular o Número de Reynolds:
Sendo: é a massa específica do ar; é a velocidade do escoamento; é o diâmetro do tubo e a viscosidade dinâmica do ar.
Devemos lembrar, também, que a velocidade do escoamento é igual à vazão volumétrica dividida pela área da seção transversal do tubo:
Ou seja, temos que o número de Reynolds é:
Pra calcular a vazão volumétrica máxima para qual o escoamento permanece laminar, devemos lembrar que, para ser laminar, o número de Reynolds deve ser .
Sendo assim temos que:
Passo 3
Pra finalizar a questão, devemos plotar em função da temperatura. Pra isso, devemos ir na Tabela A.2, intitulada “Viscosidade e massa específica do ar a 1 atm”, na página 828.
Com base nos valores de temperatura e e correspondentes, calcularemos o valor de para cada temperatura especificada. Esses cálculos estão demonstrados na tabela abaixo:
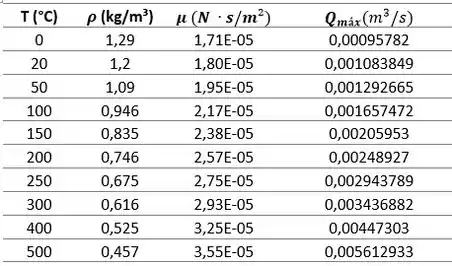
Com esses dados, podemos utilizar o Excel pra plotar um gráfico de em função da temperatura:
Como é possível notar, a plotagem não é linear. Isso ocorre porque não varia linearmente com na faixa de temperatura analisada.
Pronto, matamos a questão juntos!
Resposta
(a)
(b) A plotagem não é linear porque não varia linearmente com na faixa de temperatura analisada.