Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 5.Problemas - Ex. 87

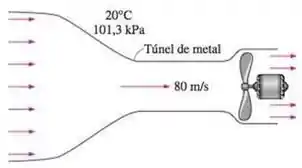
Um túnel de vento consome ar atmosférico a 20°C e 101,3 kPa por um grande ventilador localizado próximo à saída do túnel. Se a velocidade do ar no túnel é de 80 m/s, determine a pressão do túnel.

Passo 1

Oi pessoal, tudo bem?

Bem, assumimos inicialmente que:

1. O fluxo através do tubo é constante, incompressível e irrotacional com atrito desprezível (de modo que a equação de Bernoulli é aplicável).

2. O ar é e gás ideal.

E devemos lembrar que:

R a r = 0,287 k P a ⋅ m 3 k g ⋅ K

Passo 2

Pronto, agora vamos analisar o problema, ok?

Pegamos o ponto 1 no ar atmosférico antes de entrar no túnel de vento (e, portanto, P 1 = P a t m   e   V 1 ≅ 0 ) e o ponto 2 no túnel de vento. Observando que z 1 = z 2 (ou, os efeitos de elevação são desprezíveis para gases), a equação de Bernoulli entre os pontos 1 e 2 dão:

P 1 ρ g + V 1 2 2 g + z 1 = P 2 ρ g + V 2 2 2 g + z 2               → P 2 = P 1 - ρ V 2 2 2               ( 1 )

Onde:

ρ = P R T = 101,3   k P a 0,287 k P a ⋅ m 3 k g ⋅ K ⋅ 293   K = 1,205 k g m 3

Passo 3

Podemos, portanto, substituir os valores na equação 1, assim:

P 2 = 101,3 - 1,205 ⋅ 80 2 2                 → P 2 = 97,4   k P a

Resposta

Portanto: P 2 = 97,4   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Figura P4.26 são definidas coordenadas curvilíneas, ou de linha de corrente, em que n é normal à linha de corrente no plano do raio de curvatura R. A equação da quantidade de movimento sem atrito d
Como mencionado na Seção 4.10, o perfil de velocidade para escoamento laminar entre duas placas, como na Figura P4.41, é u = 4 u m á x y h - y h 2v = w = 0 á Se a temperatura em ambas as paredes é T p
Reanalise o problema 3.54 para estimar a leitura no manômetro h através da equação de Bernoulli. Para h = 58 cm do problema 3.54, qual é a perda de carga?
Ar entra em um duto de L/D = 40 a V1 = 170 m/s e T1 = 300 K. O escoamento na saída está bloqueado. Qual é o fator de atrito médio no duto para escoamento adiabático?
Ar escoa adiabaticamente por um tubo de 2 cm de diâmetro. As condições na seção 2 são p 2 = 100k P a ,T 2 = 15 º CeV 2 =170m / s º . O fator de atrito médio é de 0,024. Na seção 1, 55 metros a montant