Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 5.Problemas - Ex. 89
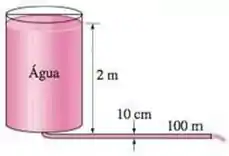
Um tanque grande com 2 m de altura é preenchido inicialmente com água. A superfície da água do tanque é aberta para a atmosfera, e um orifício com 10 cm de diâmetro e borda afiada na parte inferior drena para a atmosfera por meio de um tubo horizontal com 100 m de comprimento. Se a perda de carga irreversível total do sistema é determinada como 1,5 m, determine a velocidade inicial da água do tanque. Despreze o efeito dos fatores de correção da energia cinética.
Passo 1
Oi pessoal, tudo bem?
Bem, assumimos inicialmente que:
1. O fluxo é incompressível.
2. O tubo de drenagem é horizontal.
3. Não há bombas ou turbinas no sistema.
4. O efeito da cinética o fator de correção de energia é insignificante, α = 1.
E devemos lembrar que:
Passo 2
Pronto, agora vamos analisar o problema, ok?
Pegamos o ponto 1 na superfície livre do tanque e o ponto 2 na saída do tubo. Tomamos o nível de referência na linha central do orifício ().
Observando que o fluido em ambos os pontos está aberto para a atmosfera (e, portanto, ) e que a velocidade do fluido na superfície livre é muito baixa (V1 ≅ 0), a equação de energia entre esses dois pontos (em termos de cabeças) simplifica a:
Onde:
representa a perda de carga total do sistema.
Passo 3
Podemos, portanto, reorganizar e substituir os valores na equação 1, assim:
Resolvendo a equação, temos que:
Resposta
Portanto: