Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 5.Exercício - Ex. 5

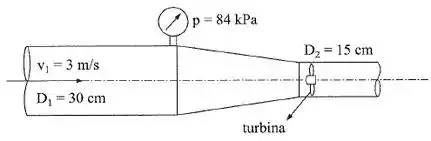
A turbina da figura ‘extrai’ a potência de 2,9 kW da água em escoamento. Desprezando as perdas na redução, calcular as forças exercidas pela água sobre a redução e sobre a turbina, respectivamente. Dados: ρ H 20 = 1000   k g / m 3 ; g = 10   m / s 2 .

Passo 1

Vamos começar o exercício analisando a parte da redução, então, como a vazão é constante entre os pontos 1 e 2, temos:

v 1 A 1 = v 2 A 2 → v 1 π D 1 2 4 = v 2 π D 2 2 4 → v 2 = v 1 D 1 2 D 2 2 = 3 0,3 2 0,15 2 → v 2 = 12   m / s

Agora vamos aplicar a equação para o equilíbrio de cargas entre os pontos 1 e 2:

H 1 = H 2

v 1 2 2 g + p 1 γ + z 1 = v 2 2 2 g + p 2 γ + z 2 → v 1 2 2 g + p 1 ρ g + z 1 = v 2 2 2 g + p 2 ρ g + z 2

Substituindo os valores conhecidos, temos:

3 2 2 10 + 84.10 3 1000 ( 10 ) + 0 = 12 2 2 10 + p 2 1000 ( 10 ) + 0 → p 2 = 1,65 10000 → p 2 = 16500   P a

Agora vamos encontrar a vazão mássica no sistema:

Q m = ρ Q 1 = ρ v 1 A 1 = ρ v 1 π D 1 2 4 = 1000 3 π 0,3 2 4 → Q m = 212   k g / s

Passo 2

A equação que representa a força que o fluido exerce é dada por:

F → s = - p 1 A 1 n → 1 + p 2 A 2 n → 2 + Q m v → 2 - v → 1

Agora vamos calcular a componente em x ( → ) :

F s x = - p 1 π D 1 2 4 - 1 + p 2 π D 2 2 4 1 + Q m v 2 - v 1

Substituindo os valores conhecidos:

F s x = - 84000 π 0,3 2 4 - 1 + 16500 π 0,15 2 4 1 + 212 12 - 3

F s x = 3740   N

Passo 3

Agora vamos analisar a parte da turbina. Para isso, vamos começar calculando a vazão do sistema:

Q m = ρ Q → Q = Q m ρ = 212 1000 → Q = 0,212   m 3 / s

Agora vamos descobrir a carga da turbina através de sua potência:

N = γ Q H T → H T = N γ Q = 2900 10 4 0,212 → H T = 1,37   m

Agora podemos aplicar o equilíbrio de cargas entre os pontos 2 e 3 para descobrir a pressão na saída:

H 2 - H T = H 3

v 2 2 2 g + p 2 γ + z 2 - H T = v 3 2 2 g + p 3 γ + z 3

Substituindo os valores conhecidos:

12 2 2 10 + 16500 10 4 + 0 - 1,37 = 12 2 2 10 + p 3 10 4 + 0 → p 3 = 2800   P a

Agora podemos analisar a força que o fluido exerce na turbina através da equação:

F → s = - p 2 A 2 n → 2 + p 3 A 3 n → 3 + Q m v → 3 - v → 2

Agora vamos calcular a componente em x ( → ) :

F s x = - p 2 π D 2 2 4 - 1 + p 3 π D 3 2 4 1 + Q m v 3 - v 2

Substituindo os valores conhecidos:

F s x = - 16500 π 0,15 2 4 - 1 + 2800 π 0,15 2 4 1 + 212 12 - 12

F s x T = 242,1   N

Resposta

F s x = 3740   N

F s x T = 242,1   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Água está escoando em regime permanente por um cotovelo de 180 ° . Na entrada do cotovelo, a pressão manométrica é 103k P a . A água é descarregada para a atmosfera. Considere que as propriedades são
Em um cotovelo redutor de 180 ° de diâmetro interno de 0,2m , a água tem uma velocidade média de 0,8m / s e uma pressão manométrica de 350k P a . Na saída, a pressão é 75k P a , e o diâmetro é 0,04m .
Água está escoa em regime permanente pelo bocal mostrado, descarregando para a atmosfera. Calcule a componente horizontal da força na junta flangeada. Indique se a junta está sob tração ou compressão.
Um grande tanque, de altura h = 1m e diâmetro D = 0,75m , está fixado sobre uma plataforma rolante conforme mostrado. Água jorra do tanque por meio de um bocal de diâmetro d = 15m m . A velocidade uni
Um jato de água saindo de um bocal estacionário a 10m / s ( A j = 0,1m 2 ) atinge uma pá defletora montada sobre um carrinho conforme mostrado. A pá vira o jato em um ângulo θ = 40 ° . Determine o val