Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 77

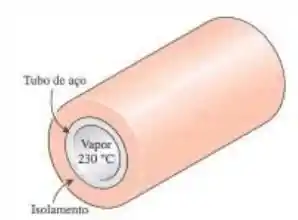
Vapor a 230°C está fluindo através de um tubo de aço k =   15,1   W   m   · ° C cujos diâmetros interno e externo são de 9 cm e 10 cm, respectivamente, em um ambiente a 13°C. O tubo é isolado com isolamento de fibra de vidro k =   0,035   W   m   · ° C   de 5 cm de espessura. Se os coeficientes de transferência de calor no interior e no exterior do tubo forem 170   e   30   W   m 2   · ° C , respectivamente, determine a taxa de perda de calor do vapor por metro de comprimento do tubo. Qual é o erro envolvido em desprezar a resistência térmica do tubo de aço nos cálculos?

Passo 1

Shoow!!

Vamos desenhar o que estamos lendo no problema:

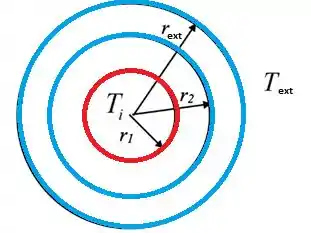
Agora que sabemos nós podemos desenhar as resistências:

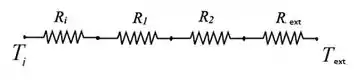
Então nós teremos aqui a resistência a convecção que é interna, seguida resistência oferecida pela camada de aço e pelo isolante. E por último nós teremos a resistência à convecção externa.

Então:

R   i = 1 h i × A i

R 1 = R c i l i n d r o , a ç o = ln ⁡ r 2 r 1 2 π k a ç o L

R 2 = R c i l i n d r o , i s o l = ln ⁡ r 3 r 2 2 π k i s o l L

R e x t = 1 h e x t × A e x t

Já sabemos como calcular as resistências, só precisamos das áreas.

Bora lá?

Passo 2

A área interna da seção transversal é dada por:

A i = π d 1 L

A i = π ( 0,0 9   m ) ( 1   m ) = 0,283   m 2

Para a área externa nós levamos em consideração o diâmetro externo do tubo de aço mais o comprimento do isolante:

d 3 = d e x t = d 2 + 2 l i s o l a n t e = 10   c m + 2 × 5   c m = 20   c m

Então:

A e x t = π d 3 L

A e x t = π ( 0,2   m ) ( 1   m ) = 0,628   m 2

Importante vocês saberem que usei o comprimento valendo 1 metro porque o enunciado pediu a taxa de perda de calor do vapor por metro de comprimento do tubo, ok?

Passo 3

Agora vamos substituir nas fórmulas e achar nossas tão queridas resistências:

R   i = 1 170 W m 2 K × 0,283   m 2 = 0,02 08   K W

R e x t = 1 30 W m 2 K × 0,628   m 2 = 0,0 53 K W

Sabendo que r = d 2 podemos adaptar as resistências:

R 1 = ln ⁡ d 2 d 1 2 π k a ç o ( 1   m )

R 2 = ln ⁡ d 3 d 2 2 π k i s o l L

Substituindo:

R 1 = ln ⁡ 0 , 10 0 , 09 2 π 15,1 W m K ( 1   m ) = 0,00 111 K W

R 2 = ln ⁡ 0 , 20 0 , 10 2 π 0 , 03 5 W m K ( 1   m ) = 3,152   K W

Como estão todas em séria, a resistência total é dada por:

R T = R i + R 1 + R 2 + R e x t

R T = 0,0208   K W + 0,00111 K W + 3,152   K W + 0,053 K W

R T = 3 , 227   K W

Passo 4

Agora sim nós conseguimos saber qual será a perda de calor para o ambiente.

Usamos a fórmula do calor:

Q ˙ = T v a p o r - T e x t R T

Substituindo:

Q ˙ = 2 3 0 ° C - 1 3 ° C 3,227   K W

Como a variação em graus Celsius e kelvin é a mesma:

Q ˙ = 67,245   W

Beleza! Achamos nossa primeira resposta!

Passo 5

A próxima pergunta é: Qual é o erro envolvido em desprezar a resistência térmica do tubo de aço nos cálculos?

Se desconsiderarmos a resistência do tubo a nova resistência total será:

R T ,   n o v a = R i + R 2 + R e x t

R T ,   n o v a = 0,0208   K W + 3,152   K W + 0,053 K W

R T ,   n o v a = 3,22 58   K W

Para saber o erro nós precisamos usar a seguinte fórmula:

ε = R T - R T ,   n o v a R T × 100 %

Substituímos:

ε = 3,227   K W - 3,2258   K W 3,227   K W × 100 %

ε = 0,0372   %

Tranquilinha?

Resposta

Calor Perdido: 67,245   W ;

Erro: 0,0372   % .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Partindo de um volume de controle diferencial em forma de uma casca esférica, desenvolva a equação da difusão térmica para um sistema unidimensional na direção radial em coordenadas esféricas com gera
Partindo de um volume de controle diferencial em forma de uma casca cilíndrica, desenvolva a equação da difusão térmica para um sistema unidimensional na direção radial em coordenadas cilíndricas com
A seção de evaporação de uma unidade de refrigeração é formada por tubos de 10m m de diâmetro com paredes delgadas, através dos quais escoa a substância refrigerante a uma temperatura de – 18 ° C . Ar
Um aquecedor elétrico delgado está inserido entre um longo bastão circular e um tubo concêntrico, com raios interno e externo iguais a 20 e 40m m , respectivamente. O bastão (A) possui uma condutivida
Um revestimento de baquelita é usado sobre um bastão condutor de 10 mm de diâmetro, cuja superfície é mantida a 200 ° C pela passagem de uma corrente elétrica. O bastão encontra-se imerso em um fluido