Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 76
O vapor superaquecido a uma temperatura de 200°C é transportado através de um tubo de aço. O tubo é isolado é isolado com uma camada de 4 cm de espessura de gesso e colocado horizontalmente dentro de um armazém onde a temperatura média do ar é de 10°C. Se os coeficientes de transferência de calor no vapor e no ar forem , respectivamente. Calcule:
- A taxa diária de perda de calor a partir do vapor superaquecido;
- A temperatura da superfície externa do isolamento de gesso.
Passo 1
Temos um problema com muita informação, né? Vamos desenhar o que estamos lendo pra facilitar nosso entendimento:
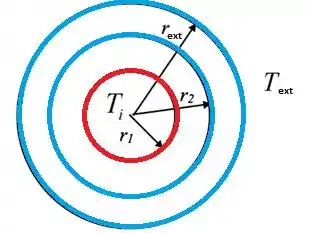
Agora que conseguimos visualizar melhor o problema, nós podemos desenhar as resistências dessa forma aqui:
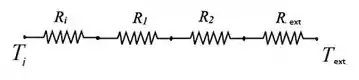
Então nós teremos aqui a resistência a convecção que é interna, seguida da resistência oferecida pela camada de aço e pelo isolante. E por último nós teremos a resistência à convecção externa, beleza?
Então, a resistência a convecção que é interna, será:
A resistência oferecida pela camada de aço, será:
A resistência oferecida pelo isolante, será:
A resistência à convecção externa, será:
Opa! Então já sabemos como calcular as resistências! Só precisamos agora encontrar as áreas.
Bora lá?
Passo 2
A área interna do tubo de aço é dada por:
Substituindo os valores, temos:
Logo:
Para a área externa nós levamos em consideração o diâmetro externo do tubo de aço mais o comprimento do isolante, ok? Ficando assim:
Teremos então:
Então a área externa será:
Com os valores, temos:
Passo 3
Agora vamos substituir nas fórmulas e achar nossas tão queridas resistências! Primeiro a resistência interna:
Agora a resistência externa:
Sabendo que podemos adaptar as resistências oferecidas pela camada de aço e pelo isolante, teremos, para a camada de aço:
E para a camada de isolante:
Substituindo em cada uma das resistências, temos, para o aço:
E para o isolante:
Como todas as resistências estão em série, a resistência total será a soma de todas elas, sendo assim:
Substituindo os valores que encontramos:
A resistência total então, será:
Passo 4
Mas não foi isso que o enunciado pediu, né? Na letra a precisamos da taxa diária de perda de calor…. E foi por isso que encontramos a resistência total! Podemos usar a seguinte relação para encontrar a perda de calor:
Substituindo os valores, temos:
Não precisa se preocupar em passar graus Celsius para kelvin, pois estamos trabalhando com a variação e ela será a mesma, temos então:
Ou podemos escrever:
Beleza! Achamos nossa primeira resposta!
Passo 5
A próxima pergunta é: Qual a temperatura da superfície externa do isolamento de gesso?
Para respondê-la basta usarmos a equação anterior para o calor, só que neste caso levaremos em conta somente a resistência convectiva externa, porque estamos falando do isolamento de gesso, ok? Ficamos então com:
Isolando a temperatura:
E substituindo os valores ficamos com:
Reparou que agora a gente precisou passar pra Kelvin, né? Show de bola, a temperatura da superfície externa do isolamento de gesso será:
Teremos, então:
E fiiim !!
Resposta
- .