Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 54
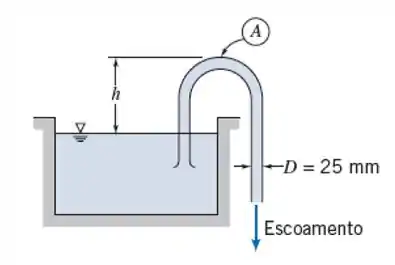
A vazão de água através do sifão é 5 L/s, a temperatura é de 20°C e o diâmetro do tubo é 25 mm. Calcule a máxima altura permitida, , de modo que a pressão no ponto A fique acima da pressão de vapor da água. (Considere o escoameto sem atrito.)
Passo 1
Beleza! Como o enunciado nos disse que a vazão no sifão é 5 L/s e nós temos o diâmetro do tubo, que é constante durante todo o trajeto, então podemos calcular a velocidade do escoamento usando a fórmula da vazão, só temos que converter ela para :
Agora, da fórmula da vazão, temos:
Passo 2
Agora vamos aplicar a equação de Bernoulli entre a superfície livre do tanque (1) e o ponto A na tubulação:
Como temos uma superfície livre no tanque, então ele está exposto à atmosfera de modo que , podemos considerar ainda que a água no tanque está parada, então temos , e para obter o valor de , devemos ir na tabela A.7 ao final do livro e pegar a pressão de vapor a 20°C, onde temos , então, substituindo os valores conhecidos na equação anterior, temos: