Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 10.Exercício - Ex. 8

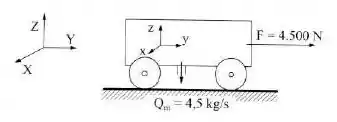
Um veículo de massa m 0 = 900   k g move-se com uma velocidade de 30   m / s em relação a um inercial, sob a ação de uma força constante de 4500   N . No instante t = 0 surge um vazamento no tanque de combustível, de forma que este é perdido verticalmente com uma vazão de 4,5   k g / s . O veículo continua a se mover sob a ação da força inicial constante. Qual será a velocidade do veículo após 20   s do início do vazamento?

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O veículo de massa inicial igual a 900   k g se move com uma velocidade inicial constante de 30   m / s . Então ocorre um vazamento no tanque e o exercício nos pede a velocidade do veículo após 20   s e g u n d o s do início do vazamento.

Bom... Sabemos do enunciado que a vazão no tanque é constante e igual a:

Q = 4,5   k g / s

Agora pensa comigo... O vazamento faz o sistema perder massa. Portanto, após 20   s a sua massa perdida será:

∆ m = Q ⋅ ∆ t

∆ m = 4,5 ⋅ 20

∆ m = 90   k g

Passo 2

Portanto a massa no segundo momento é dada por:

m 2 = m 1 - ∆ m

m 2 = 900 - 90

m 2 = 810   k g

Agora que encontramos a massa do veículo após 20   s é só aplicar a equação abaixo:

m 2 v 2 + m 1 v 1 t = F

810 v 2 + 900 ⋅ 30 20 = 4500

Isolando v 2 e resolvendo, encontraremos:

v 2 = 77,7   m / s

Resposta

v 2 = 77,7   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Óleo SAE 30W a 20°C escoa por um tubo de 9 cm de diâmetro na figura abaixo a uma velocidade média de 4,3 m/s. (a) Verifique se o escoamento é laminar. (b) Determine a vazão volumétrica em m³/h. (c) Ca
Óleo SAE 10W a 20°C escoa por um tubo horizontal reto. O gradiente de pressão é igual a 400 Pa/m. (a) Qual diâmetro D apropriado do tubo em cm se o número de Reynolds do escoamento deve ser exatamente
Um tanque de área A0 está sendo drenado em escoamento laminar por um tubo de diâmetro D e comprimento L, como mostra a figura abaixo. Desprezando a energia cinética do jato de saída e supondo que o es
Em uma certa aplicação médica, água à temperatura e pressão ambiente escoa por um canal de seção retangular de comprimento L = 10 cm, largura s = 1 cm e tamanho da folga b = 0,30 mm, como na figura ab
A spherical tank, of diameter 35 cm, is leaking air througha 5-mm-diameter hole in its side. The air exits the hole at360 m/s and a density of 2.5 kg/m3. Assuming uniformmixing, (a) find a formula for