Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 10.Exercício - Ex. 2

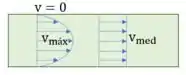
Água escoa de um tanque por um tubo lateral, conforme a figura. A velocidade do escoamento na seção do tubo de descarga é dada por: v = v m á x 1 - r R 2

Determinar:

  1. A taxa de variação com o tempo, no instante t 0 , da massa de água contida no tanque, sendo nesse instante v m á x = v m á x 0 ;
  2. A velocidade de descida no nível da água no tanque no instante inicial.

Passo 1

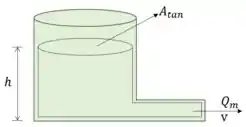
O volume do tanque é:

V t a n = A t a n ⋅ h

A área da saída é:

A = π R 2

Primeiro, vamos definir algumas relações úteis para a resolução da questão.

v m e d = 1 2 v m á x

Passo 2

Item A)

Primeiro vamos determinar o volume do tanque. Note que h varia com o tempo.

V t a n = A t a n ⋅ h

A questão pede a vazão mássica da água, então vamos considerar um volume de controle:

∂ ∂ t ∫ V C ρ ⋅ d V t a n + ∫ S C ρ ⋅ v → × n → ⋅ d A = 0

Reorganizando:

∂ ∂ t ∫ V C ρ ⋅ d V t a n = - ∫ S C ρ ⋅ v → × n → ⋅ d A

Bem, a água é por natureza um fluido incompressível, ou seja, sua densidade é constante.

ρ ⋅ d d t ∫ V C d V t a n = - ρ ⋅ ∫ S C v → × n → ⋅ d A

A velocidade de saída é normal à área. Ou seja: v → × n → = v .

ρ ⋅ d d t ∫ V C d V t a n = - ρ ⋅ ∫ S C v ⋅ d A

Resolvendo a integral de cada lado

ρ ⋅ d d t ( V t a n ) = - ρ ⋅ v m e d ⋅ A

Para o instante t 0 a velocidade é v m e d = v m á x 0 2 . Além disso, a área de saída pode ser determinada pelo seu raio

ρ ⋅ d d t ( V t a n ) = - ρ ⋅ v m á x 0 ⋅ π R 2 2

O produto ρ ⋅ d d t ( V t a n ) é a própria derivada da vazão mássica.

d Q m d t = - ρ ⋅ v m á x 0 ⋅ π R 2 2

Passo 3

Item B)

A partir da expressão:

ρ ⋅ d d t ( V t a n ) = - ρ ⋅ v m á x 0 ⋅ π R 2 2

Substituímos a expressão do volume do tanque: ρ ⋅ d d t ( A t a n ⋅ h ) = - ρ ⋅ v m á x 0 ⋅ π R 2 2

Perceba que podemos cortar as densidades. Perceba também que a área do tanque não varia.

A t a n d d t h = v m á x 0 ⋅ π R 2 2

A taxa de variação do volume da altura do tanque é:

d d t h = v m á x 0 ⋅ π R 2 2 A t a n

Resposta

  1. d Q m d t = - ρ ⋅ v m á x 0 ⋅ π R 2 2
  2. d d t h = v m á x 0 ⋅ π R 2 2 A t a n
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Com o passar do tempo, o ar escapa dos pneus de alta pressão de uma bicicleta por migração através dos poros da borracha. É regra corrente dizer que um pneu perde pressão a uma taxa de “ 6,9k P ap o r
Água escoando por um tubo com 8 c m de diâmetro entra em uma seção porosa, como mostra a figura P3.10, que permite uma velocidade radial uniforme v w através das superfícies das paredes por uma distân
Um tanque de teste de laboratório contem água do mar com salinidade S e massa específica ρ . Água entra no tanque nas condições ( S 1 ; ρ 1 ; A 1 ; V 1 ) e, por hipótese, mistura-se imediatamente no t
O escoamento no tubo na Figura P 3.12 enche um tanque de armazenagem cilíndrico conforme mostrado. No tempo t = 0 , a profundidade da água no tanque é 30c m . Calcule o tempo necessário para encher o
O recipiente cilíndrico da Figura P 3.13 tem 20c m de diâmetro e uma contração cônica no fundo com um furo de saída de3c m de diâmetro. O tanque contém água limpa nas condições padrão ao nível do mar.