Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 1.Problemas Abrangentes - Ex. 6

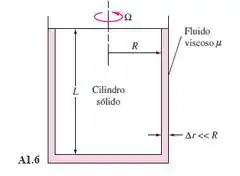
O viscosímetro de cilindro rotativo na Figura A1.6 provoca cisalhamento no fluido em uma folga pequena Δ r , como mostra a figura. Considerando uma distribuição linear de velocidade nas folgas e medindo-se o torque de acionamento M, encontre uma expressão para μ (a) desprezando e (b) incluindo o atrito no fundo.

Passo 1

Bora colocar mais uma pra conta!

Assumindo uma distribuição de velocidade linear, teremos a tensão de cisalhamento igual a:

τ = μ Δ V Δ r ≈ μ Ω r i r 0 - r i

onde Ω = v e l o c i d a d e   a n g u l a r .

A tensão causa uma força d F = τ d A = τ r i d θ L em cada elemento de superfície de área, assim, o torque dessa força é dada por d M = r i d F , logo:

M = ∫ r i d F = ∫ 0 2 π r i μ Ω r i r 0 - r i r i L d θ = 2 π μ Ω R 3 L Δ R

Isolando a viscosidade e achando a resposta da letra (a):

μ = M Δ R 2 π Ω R 3 L

Passo 2

Agora, em (b), teremos o atrito do fundo, assim:

M f u n d o = ∫ r τ d A = ∫ 0 R r μ Ω r Δ R 2 π r d r = 2 π Ω μ Δ R ∫ 0 3 r 3 d r = 2 π Ω μ R 4 4 Δ R

Portanto, o torque total será a soma do torque sem o atrito do fundo com o atrito do fundo, daí:

M t o t a l = 2 π μ Ω R 3 L Δ R + 2 π Ω μ R 4 4 Δ R

Isolando μ , teremos a resposta para (b), assim:

μ = M Δ R 2 π μ Ω R 3 L + R 4

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma placa quadrada de 1,0m de lado e 20N de peso desliza sobre um plano inclinado de 30 ° , sobre uma película de óleo. A velocidade da placa é 2m / s constante. Qual é a viscosidade dinâmica do óleo,
São dadas duas placas planas paralelas à distância de 2m m . A placa superior move-se com velocidade de 4m / s , enquanto a inferior é fixa. Se o espaço entre as duas placas for preenchido com óleo (
O pistão da figura tem uma massa de 0,5k g . O cilindro de comprimento ilimitado é puxado para cima com velocidade constante. O diâmetro do cilindro é 10c m e do pistão é 9c m e entre os dois existe u
O dispositivo da figura é constituído de dois pistões de mesmas dimensões geométricas que se deslocam em dois cilindros de mesmas dimensões. Entre os pistões e os cilindros existe um lubrificante de v
No viscosímetro da figura, o cilindro externo gira com uma rotação de 100r p m constante. O cilindro interno é oco, sua parede tem espessura desprezível e está preso a um calibrado à torção. Esse cili