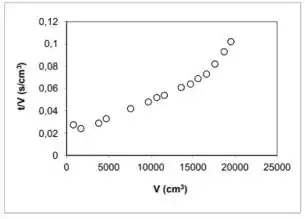
Um filtro-prensa (um quadro de ) foi utilizado na filtração, em laboratório, de uma suspensão aquosa de barita ( de sólido/L de suspensão). De acordo com a curva obtida ao se lançar versus , pede-se:
a) Estimar o parâmetro (razão entre volume de filtrado e volume de torta) para o quadro cheio.
Passo 1
Nessa questão temos que calcular a relação entre o volume de filtrado e o volume de torta, que é o .
Daí, vamos ter que usar um ponto da operação em que saibamos tanto o volume de filtrado como o volume de torta obtidos até aquele momento.
Passo 2
a) Estimar o parâmetro (razão entre volume de filtrado e volume de torta) para o quadro cheio.
Essa é bem de boas; a definição de é:
Bora obter cada um dos termos que aparece:
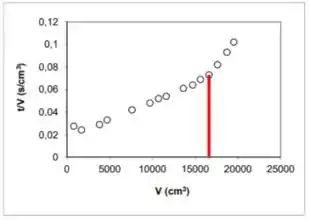
Quando o quadro está cheio, sabemos que o gráfico de sai da linearidade. Daí, podemos pegar o último ponto dentro da linearidade e estimar o valor de nesse ponto como o volume de filtrado quando o quadro enche. Usando o gráfico dado:
E, quando o quadro está cheio, o volume de torta é o próprio volume do quadro, certo? E as dimensões do quadro nós temos e são:
E sabemos também que há apenas UM quadro, daí o volume de torta, , com quadro cheio, é:
Convertendo as dimensões pra centímetros, para ficar com as mesmas unidades de :
Aí pra achar é só fazer a divisão:
Só quero fazer um comentário: nem toda área da face do quadro é disponível pra torta ocupar... somente a área efetiva! Mas NÃO temos nenhuma informação sobre a porcentagem efetiva e por isso considerei , mas saiba que é menor, ok?

SEEEE o enunciado tivesse dito a marca do quadro, poderíamos ir atrás de informações do fabricante para achar a área efetiva da face, mas não foi o caso.