Um grupo de alunos do curso de Engenharia Química da UFRJ obteve os seguintes resultados ao realizar a prática de filtração no filtro prensa do laboratório da Escola de Química:
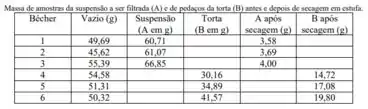
São dados:
− O experimento foi conduzido com uma suspensão aquosa de ().
− Queda de pressão no filtro: ;
− Área da face do quadro igual a e espessura do quadro igual a
− Número de quadros igual a .
− Tempo de filtração versus volume de filtrado :
![]()
Pede-se:
a) Determinar os parâmetros e .
b) Calcular a área total de filtração industrial para uma espessura de torta de e um volume final de filtrado de .
Passo 1
Vimos, na teoria, que para filtração vale:
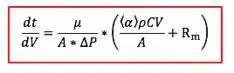
Para o caso de constante, separando o e da equação anterior e integrando:
Integrando e arrumando:
Agora temos que pegar os pontos relacionando e , plotar um gráfico e fazer regressão linear; daí tiramos os parâmetros e . Os outros termos que aparecem na equação nós temos, com exceção de e , que ainda teremos que calcular. Bora organizar nossas informações, usando tudo no sistema CGS.
Não temos porque esta é a área TOTAL de filtração, e o que nos foi dado é a área de UMA face. Para achar a área TOTAL de filtração precisamos lembrar que, em cada quadro, a área de filtração é duas vezes a área da face, pois há filtração dos dois lados no quadro. E, também, temos que multiplicar pelo número de quadros, que no caso é . Daí:
É dito que a suspensão é aquosa, mas não se fala a temperatura. Vou considerar que esteja a daí:
Passo 2
Para o cálculo da concentração , vamos usar os dados dos experimentos. A definição dessa concentração é:

Bora dar uma olhada nos experimentos relativos à concentração:

Tem 3 experimentos. Daí vamos calcular para cada um deles e depois usar a média. Organizando os cálculos numa tabela e lembrando que:

Usando a média desses três:
Passo 3
- Determinar os parâmetros e .
Como já vimos lá no passo 1, temos que plotar e fazer regressão linear. Usando as unidades do CGS, isto é, tempo sem segundos e volume em , os dados plotados ficam:
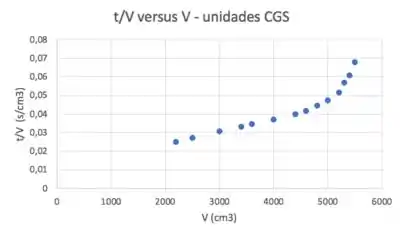
A regressão linear fazemos só com a parte linear do gráfico, lembra? Os outros pontos nós descartamos. Vou pegar até o ponto com porque está bemmm linear haha
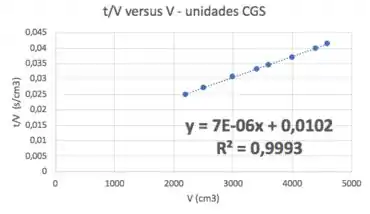
Agora é só comparar a equação obtida com a regressão com a desenvolvida teoricamente:
Isto é:
Daí:
E
Usando tudo no CGS, temos:
E
Isolando-os e fazendo as continhas:
Passo 4
b) Calcular a área total de filtração industrial para uma espessura de torta de e um volume final de filtrado de .
Agora temos que projetar um filtro industrial baseado nesses experimentos aí. Podemos escrever a área total de filtração industrial e função das medidas na escala piloto como:
E temos que:
Pelo gráfico do experimento, vemos que o gráfico foge da linearidade em , daí:
E o enunciado pede que:
Daí:
Resposta
- e