Um filtro-prensa (um quadro de xx) foi utilizado na filtração, em laboratório, de uma suspensão aquosa de barita ( de sólido/L de suspensão). De acordo com a curva obtida ao se lançar versus , pede-se:
Calcular os parâmetros e ; caso dependam de parâmetros desconhecidos, deixar indicado o cálculo.
OBS:
- A lavagem não é necessária;
- O tempo de desmantelamento, limpeza e montagem é estimado em .
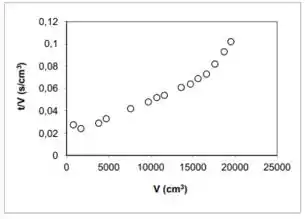
Considere a área de filtração igual a:
Passo 1
Lá na teoria, vimos que, partindo da equação do movimento, chegamos na equação de trabalho para filtração:
E, integrando-a ao longo do filtro, à constante, chegamos em:
Essa equação aí representa uma reta e podemos usá-la pra determinar parâmetros com base em experimentos, que é exatamente o que essa questão pede :) Mas temos que lembrar de só pegar os pontos que estão alinhados no gráfico!
As informações de lavagem e tempo de desmantelamento, limpeza e montagem não vamos usar pra nada, mas repara que aparece a concentração na fórmula da reta que achamos:
E essa concentração temos como calcular já que:

Passo 2
A primeira coisa que vou fazer é calcular logo a concentração :

Nos foi informado que a suspensão de trabalho é aquosa e de barita, com concentração de sólido/L de suspensão. Daí:
Nesse 1 litro de suspensão, sabemos a massa de sólido, . Usando a densidade da barita, determinamos esse volume de sólido :
Daí:
A densidade da barita não foi dada, mas é tabelada então temos como achar:
Só lembrar que, como a massa está em gramas, vamos usar a densidade em , para ficar com unidades compatíveis. Daí o volume vai sair em .
Ok, tendo o volume de sólidos, podemos calcular o volume de água:
Como volume de sólidos está em , vou passar o litro pra também, pra deixar tudo com mesmas unidades, né.
Ok, mas para calcular precisamos da MASSA de líquido, e não do volume... Novamente, usamos densidade, mas agora a da água:
A densidade da água varia com a temperatura e, como não temos a temperatura, poderíamos fazer duas coisas:
- Assumir que a densidade da água é por volta de então usar esse valor
- Deixar a densidade indicada
Como o enunciado disse para deixar indicado o que fosse desconhecido, vou pelo segundo caminho.
De qualquer maneira, como “temos” a massa de sólidos e a de água, podemos calcular :

Passo 3
Agora que já calculamos a concentração , podemos partir pra análise do gráfico:
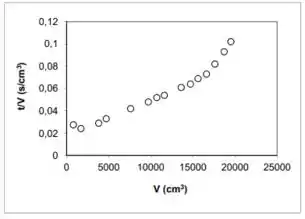
Vimos que a parte LINEAR pode ser descrita por:
Comparando essa equação com à de uma reta:
Temos que o coeficiente angular é:
E o coeficiente linear é:
Agora, traçamos a melhor reta possível para os dados na parte linear; como já temos o gráfico, não vale a pena pegar ponto a ponto e fazer regressão linear; mais vale traçar a reta na mão mesmo, ou no computador no caso hahah
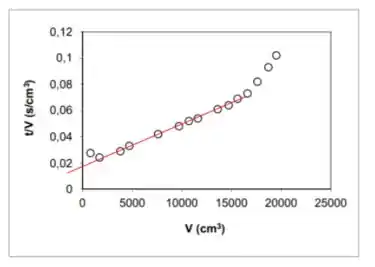
E foi assim que EU tracei... Se você tiver traçado um pouco mais pra cá, ou um pouco mais pra lá, tá de boas; só tem que lembrar de desprezar o primeiro ponto e os últimos 3, porque fogem da linearidade.
Agora, vendo pelo gráfico, podemos pegar os coeficientes linear e angular. Começando pelo linear, que é o valor de quando a reta cruza o eixo , isto é, quando :
Já o angular, pegamos pela tangente da reta com o eixo x. Temos que usar pontos em cima da reta que traçamos!!! E NÃO necessariamente pontos experimentais, ok? Vou usar, para o cálculo, os pontos:
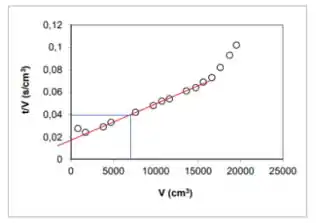
Passo 4
Acabamos de calcular os coeficientes linear e angular da reta experimental:
Agora, comparamos os valores calculados com a expressão pra cada um deles:
Daí:
Nos é pedido pra calcular os parâmetros e , daí bora isolá-los nessas expressões:
E agora é só substituir tudo que temos, que no caso são só:
Daí:
E é só até aqui que conseguimos chegar com os dados fornecidos.