Baseado nos experimentos abaixo apresentados, calcule a porosidade da torta.
Dados:
- O experimento foi conduzido com uma suspensão aquosa de ()
- Considere a densidade da água igual a
Passo 1
Essa questão é mais de porosidade do que de filtração, hein. Mas ela é importante aqui pra fixarmos quais informações usar em cada momento... Primeiro, precisamos lembrar da definição de porosidade:
O “vazio” aqui vai ser a água e o “cheio” são as partículas. O lance é escrever o total como:
Daí:
E, como temos informações de massas e não volumes, usamos a densidade:
Rearranjando:
Daí, para a água e para partículas, vamos ter, respectivamente:
Substituindo isso na fórmula da porosidade que já chegamos:
E é essa fórmula que vamos ter que usar.
Passo 2
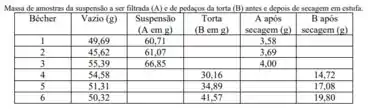
Ok. Já temos a fórmula pra achar a porosidade, mas há dois tipos de experimento na tabela:
- Pesagem de suspensão com a água e depois de seca
- Pesagem da torta úmida e dela depois de seca
Queremos calcular a porosidade da torta então só o que nos interessa são os experimentos com torta úmida e seca.
Além disso, há 3 experimentos desse tipo, daí temos que calcular a porosidade por cada um deles e a resposta será uma média dos 3 resultados. Acho melhor organizar isso numa tabela, não?
Ahhh, e temos a massa de torta úmida (água + partículas) e a massa de torta seca (apenas partículas), aí tiramos a massa de água por diferença:
Passo 3
Usando a fórmula que vimos lá no passo 1:
Substituindo as densidades e escolhendo o CGS pra trabalhar:
Só vamos usar os experimentos com torta, daí, só os resultados 4, 5 e 6 nos interessam:
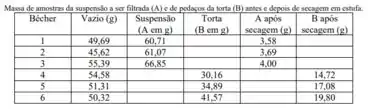
Pelo experimento 4:
Daí:
Calculando para os 3 experimentos de torta:
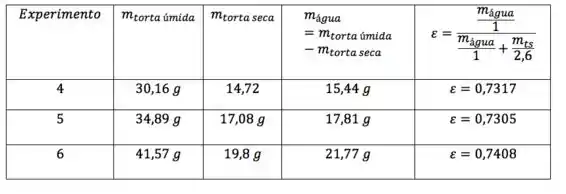
Fazendo a média dos três resultados:
É importante levar várias casas decimais nesses casos de múltiplos experimentos pra não acabar aproximando tudo pro mesmo valor e aí a média ficar sem sentido depois.