Uma certa suspensão é filtrada a pressão constante em um filtro-prensa com quadros de 1” de espessura. Em de operação, os quadros ficam cheios e o volume de filtrado obtido é de de área filtrante. Determinar a produção de filtrado, em de filtrado por de área de filtrante por tempo total de um ciclo quando a mesma suspensão e nas mesmas condições é filtrada em filtro com quadros de de espessura. O volume de água de lavagem (placas de 3 botões) deve ser igual ao volume da torta e o tempo de desmantelamento, limpeza e montagem é de .
Passo 1
Esse problema é de mudança de escala; um detalhe é que ele está diminuindo a escala e não aumentando, mas isso é indiferente pra gente. O filtro com quadros de é o nosso piloto e o com é o industrial.
Dentre outros dados, o enunciado diz que tem placa de 3 botões na lavagem, daí é lavagem completa! E ele diz também que:
Ou seja, o volume de água de lavagem é igual ao volume da torta, no filtro industrial.
E repara que ele já deu o tempo de desmantelamento, limpeza e montagem:
Geralmente os enunciados dão o porque a gente não tem equação pra ele; depende muito da realidade de cada fábrica.
A produção é o quanto de filtrado a gente tem pelo tempo necessário pra obter ele. Pra calcular isso, vamos precisar do volume de filtrado e os tempos de filtração, lavagem e desmantelamento.
Bora agora estudar esse filtro, lembrando que vamos trabalhar com aquelas equações independentes.
Passo 2
Vamos começar calculando o tempo de filtração:
Vou trabalhar com hora, daí:
Beleza! Já temo o tempo de filtração e o de desmantelamento. Só falta o de lavagem.
Calculando o tempo da lavagem completa:
Como e :
Eu usei o industrial para os dois aqui. Tanto faz já que e são constantes no industrial e piloto, mas peguei o industrial porque tenho outras informações pra ele. Saca só:
Onde a gente divide a área por dois porque a área de filtração são as duas faces do quadro. E pra calcular o volume a gente precisa da área de uma face só, valeu?
Então ficamos com o seguinte:
E por que só substituímos um e não os dois? Porque, pro filtro industrial, nos foi dado que . Foi por isso que optamos por usar os e do industrial, e não do protótipo 😉. Substituindo isso:
Agora, qual a relação entre o volume de filtrado e a área filtrante?
Pro protótipo nós sabemos que:
E a área de filtração industrial é dada por:
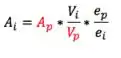
Isolando o :
Então:
Ufa, agora o tempo de lavagem sai:
Show, já temos os três tempos! Bora calcular a produção!

Passo 3
O que o enunciado pede é a produção de filtrado, em de filtrado por de área de filtrante por tempo total de um ciclo, isto é:
Aquele ali a gente já teve que calcular.
E os tempos também já calculamos, fora o que foi dado mesmo.
Daí: