Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Aceleração Angular

Ver Todos os Exercícios

Teoria

Sempre que temos um movimento circular onde a velocidade varia ao longo do tempo, temos uma aceleração angular e é sobre ela que vamos conversar hoje! 😉

Como Calcular a Aceleração Angular

Lá na cinemática retilínea a gente calculava a aceleração média a partir da variação da velocidade em relação ao tempo, lembra? Mas e agora, como fazemos?

O raciocínio aqui é o mesmo! A única diferença é que ao invés de usarmos a variação de velocidade escalar, usamos a variação de velocidade angular , assim:

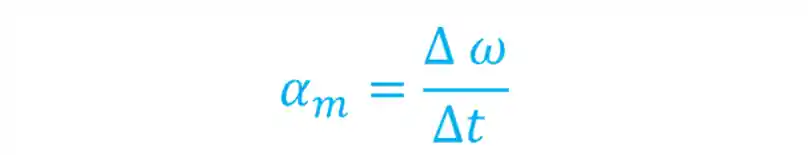
Aceleração angular média
Aceleração angular média

Onde:

  • é a aceleração angular média, em ;
  • é a variação da velocidade angular, em ;
  • é a variação de tempo, em .

📢 Clique para ver mais:

Aceleração Angular Instantânea

Mas e se quisermos saber a aceleração angular de um corpo em um momento exato e não sua média?!

É ai que entra a aceleração angular instantânea! Nela a variação de tempo é muito pequenininha, tão pequenininha que podemos aproxima-la de zero. Então calculamos usando a derivada da velocidade angular em relação ao tempo, assim:

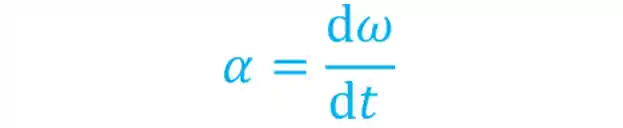
Aceleração angular instantânea
Aceleração angular instantânea

Uma outra forma de calcular a aceleração angular instantânea, que é usando o deslocamento angular:

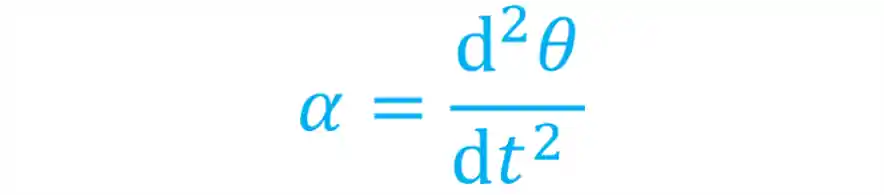
Aceleração angular instantânea a partir de
Aceleração angular instantânea a partir de

Na verdade essas duas fórmulas são iguais, tudo o que fizemos foi substituir usando a fórmula da velocidade instantânea, que aliás, vamos falar dela jájá!

Mas agora, se liga nesse vídeo que o Responde Aí preparou pra você. Nele a gente fala das fórmulas de velocidade e aceleração angular instantâneas como usamos elas nos exercícios! Dá só uma conferida! 👇

Velocidade Angular

A velocidade angular média é calculada a partir do deslocamento angular em relação ao tempo, como podemos ver na fórmula abaixo:

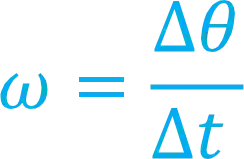
Aceleração angular média.
Aceleração angular média.

Onde:

  • é a velocidade angular média, em ;
  • é o deslocamento angular, em ;
  • é a variação de tempo, em .

Velocidade Angular Instantânea

Pra a gente saber a velocidade angular de um objeto em um momento específico, usamos a velocidade angular instantânea. O raciocínio é o mesmo da aceleração instantânea, consideramos um intervalo de tempo bem pequenininho, tendendo a zero.

A fórmula fica com essa carinha aqui:

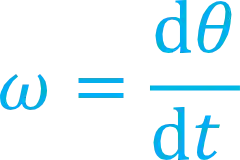
velocidade angular instantânea
velocidade angular instantânea

Agora vamos praticar com exercícios?

Velocidade Angular

Exercícios Resolvidos

Exercício Resolvido #1

UVA- 2016- Lista 3- Questão 7- Prof Otávio Castellani

Durante um intervalo de tempo t, o volante de um gerador gira de um ângulo e θ = a t + b t 3 - c t 4 , onde a , b e c são constantes. Escreva expressões para o vetor velocidade angular

Passo 1

Bom, sabemos a relação da velocidade angular com o deslocamento angular:

ω = d θ d t

Portanto, para obtermos a expressão da velocidade angular, basta derivarmos a expressão do deslocamento. Então:

ω t = a + 3 b t 2 - 4 c t 3

Tranquilo, né?

Resposta

ω = a + 3 b t 2 - 4 c t 3

Exercício Resolvido #2

UVA- 2016- Lista 3- Questão 10- Prof Otávio Castellani

A posição angular de um ponto sobre uma roda que está girando é dada por θ = 2 + 4 t 2 + 2 t 3 , onde θ está em radianos e t em segundos. Em t = 0 , qual é a posição angular do ponto ?

Passo 1

Temos a expressão de θ em função do tempo, certo? Para obter o θ em um tempo específico, basta substituir, se liga:

θ 0 = 2 + 4   .   0 2 + 2   .   0 3 = 2   r a d

Resposta

a )   2   r a d

Exercício Resolvido #3

Halliday 9ª edição vol.1 cap.10 seção 2 questão 8

A aceleração angular de uma roda é a   =   6,0 t 4   - 4,0 t 2 , com a em radianos por segundo ao quadrado e tem segundos. No instante t   = 0 , a roda tem uma velocidade angular de + 2,0   r a d / s e uma posição angular de +   1,0   r a d . Escreva expressões

a) para a velocidade angular (em r a d / s ) e

b) para a posição angular (em r a d ) em função do tempo (em s ).

Passo 1

Integrando em relação ao tempo a expressão dada para a aceleração e levando em conta que a velocidade inicial é 2,0   r a d / s , obtemos:

ω   =   1,2 t 5   – 1,33   t 3   +   2,0

Passo 2

E agora, integrando novamente e levando em conta que a posição angular inicial é 1   r a d , obtemos;

θ   =   0,20 t 6   –   0,33   t 4   +   2,0   t   +   1,0

Resposta

ω   =   1,2 t 5   – 1,33   t 3   +   2,0

θ   =   0,20 t 6   –   0,33   t 4   +   2,0   t   +   1,0

Tranquilo galera? Bora resolver mais questões então

Exercício Resolvido #4

Halliday 9ª edição vol.1 cap.10 seção 2 questão 4

A posição angular de um ponto de uma roda é dada por θ   =   2,0   +   4,0 t 2   +   2,0 t 3 , onde θ está em radianos e t em segundos. Em t   = 0 , qual é:

a) a posição angular no ponto?

b) a velocidade angular do ponto?

c) Qual éa velocidade angular em t   =   4,0   s ?

d) Calcule a aceleração angular em t   =   2,0   s .

e) A aceleração angular da roda é constante?

Passo 1

Fazendo t   =   0 na função dada, obtemos θ 0   =   2,0   r a d .

Passo 2

Ec omo sabemos, a velocidade angular em função do tempo é dada por:

ω = d θ d t = 8 t + 6 t 2

Fazendo   t   =   0   na função acima, obtemos ω 0   =   0 .

Passo 3

Para t   =   4,0   s , função do item (b) nos dá :

ω 4   =   8,0 4,0 +   6,0 4,0 2   =   128 r a d s =   1,3 *   10 2   r a d / s

Passo 4

A aceleração angular em função do tempo é dada pela derivada da velocidade angular em função do tempo, então:

α = d ω d t = 8 + 12 t

Para t   =   2,0 , a equação acima nos dá α 2   =   8,0   +   ( 12,0 ) ( 2,0 )   =   32   r a d / s 2 .

Passo 5

De acordo com a equação obtida no item (d), a aceleração angular varia com o tempo e, portanto, não é constante.

Resposta

θ 0   =   2,0   r a d

ω 0   =   0

ω 4 =   1,3 *   10 2   r a d / s

α 2     =   32   r a d / s 2

De acordo com a equação obtida no item (d), a aceleração angular varia com o tempo e, portanto, não é constante.

Tranquilo galera? Bora resolver mais questões então

Exercício Resolvido #5

Halliday 9ª edição vol.1 cap.10 seção 5 questão 20

Um objeto gira em torno de um eixo fixo e a posição angular de uma reta de referência sobre o objeto é dada por θ =   0,40 e 2 t , onde θ está em radianos e t   em segundos. Considere um ponto do objeto situado a 4,0   c m do eixo de rotação . Em t   = 0   , qual é o módulo

a) da componente tangencial no ponto?

b) da componente radial da aceleração do ponto?

Passo 1

A função θ = ζ e β t   é usada para descrever a posição angular de uma reta.

Ele quer informações a respeito da aceleração.

Sabemos que:

α = d 2 θ d 2 t

Derivando a função duas vezes em relação ao tempo, obtemos:

ω = d θ d t = ζ β e β t   e     α = d 2 θ d 2 t = ζ β 2 e β t

Show! Já sabemos o mósulo da aceleração angular. Vamos lembrar de mais umas relações aqui:

α t = α r

Como vimos α = d 2 θ d 2 t

Então:

α t = α r

α t = d 2 θ d 2 t r

Substituindo:

α t = ζ β 2 e β t r

Fazendo r   =   0,04   m , ζ   =   0,40   m , β   =   2   s - 1 e t   =   0 , obtemos α t   =   0,064   m / s 2 .

Passo 2

Como a gente já viu, α r = ω 2 r = r d θ d t 2 = r ζ 2 β 2 e 2 β t .

Fazendo r   =   0,04   m , ζ   =   0,40   m , β   =   2   s - 1 e t   =   0 , obtemos α r =   0,026   m / s 2 .

Resposta

α t   =   0,064 m s 2

α r =   0,026   m / s 2

Exercício Resolvido #6

Halliday 9ª edição vol.1 cap.10 seção 5 questão 22

Um astronauta está sendo testado em uma centrífuga. A centrífuga tem um raio de 10   m e, partindo do repouso, gira de acordo com a equação θ = 0,30 t 2 , onde   t está em segundos e θ em radianos. No instante t   =   5,0   s , calcule o módulo

a) da velocidade angular

b) da velocidade linear

c) da aceleração tangencial

d) da aceleração radial do astronauta

Passo 1

Bom, de acordo com o que vimos, a velocidade angular no instante t   =   5,0   s é

ω = d θ d t t = 5 s = d d t ( 0,30 t 2 ) t = 5 s = 2 0,30 5 = 3 r a d s

Passo 2

E agora, a velocidade linear no instante t   =   5,0 s é

v = ω r = 3 r a d s 10 m = 30 m s

Passo 3

E agora, pra aceleração angular, temos:

α = d ω d t = d d t 0,60 t = 0,60 r a d / s 2

E a aceleração tangencial é:

α t = r α = 10 m 0,60 r a d s 2 = 6 m / s 2

Passo 4

E a aceleração radial ou centrípeta é calculada por:

a r = ω 2 r = 3 r a d s 2 10 m = 90 m / s

Resposta

ω = 3 r a d s

v = 30 m s

α t = 6 m / s 2

a r = 90 m / s

Tranquilo galera? Bora resolver mais questões então

Exercício Resolvido #7

Elaboração Própria

Uma partícula tem uma aceleração angular que varia com o tempo conforme a equação: α = 6 t + 3 t 2 .

a) Encontre a velocidade angular em função do tempo t .

b) Encontre o valor dessa aceleração e da velocidade angular no instante t=2s.

Passo 1

Aqui devemos lembrar que

α = d ω d t

Então pra gente encontrar a velocidae angular a partir da equação da aceleração angular, devemos integrar, ou seja:

ω = ∫ α d t

Passo 2

Integrando a equação dada pela questão, temos:

α = 6 t + 3 t 2

∫ α d t = ∫ 6 t + 3 t 2 d t

ω = 3 t 2 + t 3

Prontinho!

Passo 3

Agora aplicando o tempo de 2 segundos pra descobrirmos a velocidade angular e a aceleração angular instantâneas, temos:

ω = 3 t 2 + t 3 = 3.2 2 + 2 3 = 20 r a d / s

α = 6 t + 3 t 2 = 6.2 + 3.2 2 = 24 r a d / s 2

Conseguimos!

Resposta

  1. ω = 3 t 2 + t 3
  2. ω = 20 r a d / s   e α = 24 r a d / s 2

Exercício Resolvido #8

Elaboração Própria

Uma partícula tem sua posição angular que varia com o tempo conforme a equação: θ t = 18 t 3 + 12 t 5 + 3 t 2 .

  1. Encontre a velocidade angular em função do tempo t .
  2. Encotnre a aceleração angular em função do tempo t .

c) Encontre o a posição, a velocidade e a aceleração angular no instante t=1s.

Passo 1

Como a gente já viu:

ω = d θ d t

Então vamos derivar a equação da posição pra descobrirmos a velocidade, né? Bora lá:

θ t = 18 t 3 + 12 t 5 + 3 t 2

d θ d t = ω ( t ) = 54 t 2 + 60 t 4 + 6 t

Passo 2

E agooora, pra gente encontrar a celeração angular, temos que:

α = d ω d t

Prontinho, agora vamos derivar:

ω ( t ) = 54 t 2 + 60 t 4 + 6 t

d ω d t = α ( t ) = 108 t + 240 t 3 + 6

Showw!

Passo 3

Pra encontrar a posição, velocidade e aceleração angulares nesse instante devemos só susbtituir o valor do tempo nas equações, então:

θ 1 = 18 . 1 3 + 12 . 1 5 + 3 . 1 2 = 33 r a d

ω 1 = 54 . 1 2 + 60 . 1 4 + 6 . 1 = 120 r a d / s

α 1 = 108 . 1 + 240 . 1 3 + 6 = 354 r a d / s 2

Showw! Acabamos!

Resposta

  1. ω ( t ) = 54 t 2 + 60 t 4 + 6 t
  2. α ( t ) = 108 t + 240 t 3 + 6
  3. θ = 33 r a d , ω = 120 r a d / s e α = 354 r a d / s 2

Exercícios de Livros Relacionados

A posição angular de um ponto de uma roda é dada por θ=2,0+4,0 t 2+2,0 t 3 , onde θ está em radianos e t em segundos. Em t= 0 , qual é (a) a posição e (b) a velocidade angular do ponto? (c) Qual éa ve
Um disco com raio igual a 25,0c m está livre para girar em torno de um eixo perpendicular a ele e que passa pelo seu centro. Ele possui um fio delgado, porém forte, enrolado em torno da sua borda e o
Um bom lançador de beisebol pode arremessar uma bola a 85 m i / h com uma rotação de 1800r e v / m i n . Quantas revoluções a bola realiza até chegar à base principal? Para simplificar, suponha que a
Uma polia com 8,0c m de diâmetro tem uma corda de 5,6m de comprimento enrolada na borda. Partindo do repouso, a roldana recebe uma aceleração angular constante de 1,5r a d / s 2 , (a) que ângulo a rol
Quando uma torrada com manteiga é deixada cair de uma mesa, adquire um movimento de rotação. Supondo que a distância da mesa ao chão é 76c m e que a torrada não descreve uma revolução completa, determ