Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 9.Problemas - Ex. 67

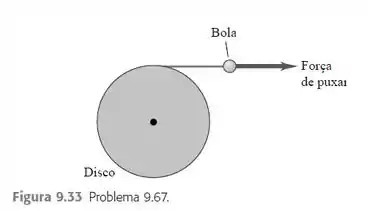
Um disco com raio igual a 25,0   c m está livre para girar em torno de um eixo perpendicular a ele e que passa pelo seu centro. Ele possui um fio delgado, porém forte, enrolado em torno da sua borda e o fio está preso a uma bola que é puxada tangencialmente afastando-se da borda do disco ( F i g u r a   9.33 ). O módulo da força de puxar aumenta e produz uma aceleração da bola, que segue a equação a t = A t , onde t está em segundos e A é uma constante. O cilindro parte do repouso e, ao final do terceiro segundo, a aceleração da bola é 1,80   m / s 2 . a) Determine A. b) Expresse a aceleração do disco em função do tempo. c) Quanto tempo depois de começar a girar o disco atinge uma velocidade escalar angular de 15,0   r a d / s ? d) Qual é o ângulo do giro do disco ao atingir 15,0   r a d / s ? (Sugestão: Veja a Seção 2.6.)

Passo 1

Oi, galerinha! Tudo bom?

A aceleração angular α (aqui é a letra grega alfa) do disco está relacionada à aceleração linear a (aqui é a letra a mesmo) da bola por:

a = R α

Agora vamos lembrar que a aceleração é a variação da velocidade pelo tempo, então podemos pensar que a velocidade é a integral da aceleração em um espaço de tempo. E por que estou falando isso?

Como a aceleração não é constante, vamos usar:

ω - ω 0 = ∫ 0 t α d t

Do mesmo modo, que para relação da velocidade e variação angular (deslocamento), teremos:

θ - θ 0 = ∫ 0 t ω d t

Assim estamos relacionando θ , ω , α e t   para o disco.

Lembrando como realizar uma integral de potencia:

∫ t n d t = t n + 1 n + 1

Veja só!

Passo 2

Agora vamos separar os dados:

Em a = R α , α é dado em r a d / s 2

O cilindro parte do repouso, então: ω 0 = 0

Ao final do terceiro segundo significa que t = 3 s

A aceleração é: a = 1,80   m / s 2

Agora bora aplicar tudo!

Passo 3

  1. Queremos determinar A da função a t = A t , isso implica que:

    2. A = a t = 1,80 m s 2 3 s

    A = 0,600 m / s 3

    Tranquilo até aqui?

    Passo 4

  2. E então para calcularmos α , partimos da equação:

    3. a = R α

    Isso implica que:

    α = a R = 0,600 m s 3 t 0,250 m

    α = 2,40 r a d / s 3 t

    Bacana, não é?

    Passo 5

  3. Então, vamos calcular ω , fazendo

    4. ω - ω 0 = ∫ 0 t α d t

    pois a aceleração varia.

    Como ω 0 = 0 e encontramos α = 2,40 r a d / s 3 t , ficamos com:

    ω = ∫ 0 t 2,40 r a d / s 3 t d t = 2,40 r a d / s 3 ⋅ t 2 2

    ω = 1,20 r a d / s 3 ⋅ t 2

    Pronto, temos que ω = 2,40 r a d / s 3 ⋅ t 2 .

    E sabemos que a velocidade escalar atinge ω = 15 r a d / s .

    Então, basta isolarmos t . Dessa forma:

    t = 15 r a d / s 1,20 r a d / s 3 = 3,54 s

    Show?

    Passo 6

  4. E para calcularmos o ângulo de giro, calculamos através da equação:

θ - θ 0 = ∫ 0 t ω d t

Portanto, temos que:

θ - θ 0 = ∫ 0 t 1,20 r a d / s 3 ⋅ t 2 d t = 1,20 r a d / s 3 ⋅ t 3 3 = 0,400 r a d / s 3 t 3

Então, para t = 3,54 s :

θ - θ 0 = 0,400 r a d / s 3 ( 3,54 s ) 3

θ - θ 0 = 17,7 r a d

E aí! Entendeu tudo? Responde Aí!

Resposta

  1. A = 0,600 m / s 3
  2. α = 2,40 r a d / s 3 t
  3. t = 3,54 s
  4. θ - θ 0 = 17,7 r a d
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma polia com 8,0c m de diâmetro tem uma corda de 5,6m de comprimento enrolada na borda. Partindo do repouso, a roldana recebe uma aceleração angular constante de 1,5r a d / s 2 , (a) que ângulo a rol
Uma técnica está testando um motor de velocidade variável, controlado por computador. Ela prende um disco fino ao eixo do motor, com o eixo no centro do disco. Este parte do repouso e sensores ligados
Um disco uniforme com raio R 0,400 m e massa de 30,0 kg gira em um plano horizontal sobre um eixo vertical sem atrito, que passa pelo centro do disco. O ângulo através do qual o disco gira varia com u
Em um CD, a música é codificada em uma configuração de minúsculos sulcos dispostos ao longo de uma trilha que avança formando uma espiral do interior à periferia do disco. À medida que o disco gira no
Se a hélice de um avião gira a 2000r e v / m i n quando o avião voa com uma velocidade de 480k m / h em relação ao solo, qual é a velocidade escalar linear de um ponto na ponta da hélice, a 1,5m de di