Velocidade e Aceleração Médias no Movimento Circular
Produzido por Ludovic BeghinTeoria
Velocidade Média e Aceleração Média no Movimento Circular
Estudaremos agora a velocidade média e a aceleração média no Movimento Circular Uniforme.
Velocidade Média
Sabemos que a fórmula de velocidade média é:
Agora, como a aplicaremos no movimento circular uniforme?
Vamos pensar primeiro no , ou seja, o deslocamento que a partícula faz em um movimento circular. No movimento circular, ele é calculado da mesma forma, .
Exemplo:
Uma partícula que faz um movimento no sentido anti-horário de 1/4 de círculo, terá o da seguinte forma, representado pela setinha azul:
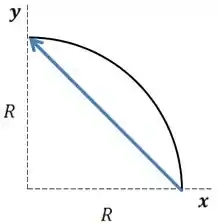
Nesse caso, para descobrirmos o valor de seu módulo, podemos fazer Pitágoras.
Show!
E o ?
Como a velocidade escalar é constante, podemos descobri-lo por meio da fórmula que relaciona distância percorrida com o tempo.
A distância percorrida vai ser o comprimento do círculo que a partícula percorreu.
No exemplo acima, a distância percorrida é do comprimento do círculo de raio .
Sabendo que o comprimento de um círculo completo é então:
Logo:
Após acharmos os valores de e , podemos substituir na fórmula inicial e achamos o valor da velocidade média.
No exemplo que estudamos, o módulo é igual a:
Tranquilo, né? Esse é o tipo de coisa que não é tão intuitivo, mas é tranquilo de aprender.
Aceleração média
A aceleração média é calculada por:
O passo a passo para achar seu módulo é o mesmo que o utilizado para achar o módulo da velocidade média. Lembre-se que a aceleração média é dada que sabemos os pontos inicial e final que queremos =D
Passo 1: Achar por meio dos vetores. Aplicando
Passo 2: Achar da mesma forma que no caso da velocidade média.
OBS: A velocidade no Movimento Circular Uniforme é constante, a aceleração que existe é a centrípeta, ela não altera o módulo da velocidade tangencial, beleza? Então podemos aplicar e, consequentemente
Passo 3: Substituir os valores encontrados na fórmula inicial
É isso! Agora vamos praticar nos exercícios!
Aceleração média
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ, Física 1, Prova 1, 2012.1
Uma partícula descreve um movimento circular, com velocidade de módulo constante e igual a . Num intervalo de tempo em que percorre da circunferência, o módulo de seu vetor velocidade média é igual a
Passo 1
Os dados do enunciado são
O vetor velocidade média é
Vamos fazer um esboço do movimento, considerando o raio do movimento .
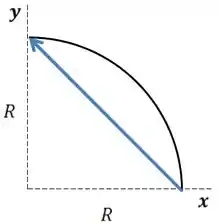
Vamos considerar que o corpo está girando no sentido anti-horário.
Passo 2
O vetor em azul, é o vetor deslocamento, como ele quer o módulo do vetor velocidade média devemos ter o módulo do vetor deslocamento.
Passo 3
Então
Porém, não temos nenhuma dessas variáveis.
Passo 4
Sabemos que o módulo da velocidade é ,
Como a velocidade é constante
Onde é a distancia percorrida, que nesse caso é do comprimento do círculo de raio .
O comprimento de um circulo completo é então
Passo 5
Substituindo na equação do módulo da velocidade média
- ''Resposta
Letra A
Exercício Resolvido #2
UFRJ, Física 1, Prova 1, 2014.1
Uma partícula descreve um movimento circular de raio , com velocidade de módulo constante e igual a . Num intervalo de tempo em que percorre da circunferência, o módulo de seu vetor aceleração média é
- ;
- ;
- ;
- ;
- ;
Passo 1
Os dados do problema são
Para acharmos o vetor aceleração média temos
Devemos então achar .
Passo 2
Vamos fazer um esboço de como é esse movimento, como ele está com um movimento circular a velocidade é tangente ao círculo.]
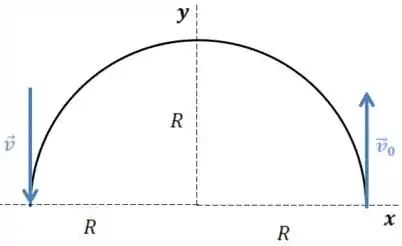
Repare que, sabendo que o módulo das velocidades é ,
Uma está apontando para cima, logo positiva, enquanto outra está apontando para baixo, logo negativa.
Passo 3
Voltando a fórmula do vetor aceleração média
O módulo do vetor aceleração media é
Porém não temos
Passo 4
Sabemos que o módulo da velocidade é ,
Como a velocidade é constante
Onde é a distancia percorrida, que nesse caso é do comprimento do círculo de raio .
O comprimento de um circulo completo é então
Passo 5
Queremos , então
Passo 6
Substituindo na fórmula do módulo da aceleração vetorial
Resposta
Letra B
Exercício Resolvido #3
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 1 , 8º ed. Rio de Janeiro: LTC , 2008, pp 88- 68
Um gato pula em um carrossel que está descrevendo um movimento circular uniforme. No instante a velocidade do gato é , medida em um sistema de coordenadas horizontal. No instante a velocidade é Quais são:
- o módulo da aceleração centrípeta do gato.
- a aceleração média do gato no intervalo de tempo , que é menor que um período.
Passo 1
Vamos lá, galera!
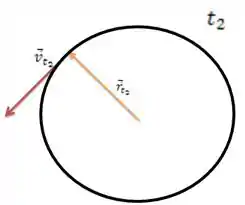
Como ele nos diz que temos um MCU, no tempo e no tempo teremos as velocidades e o vetor posição , como mostrado abaixo.
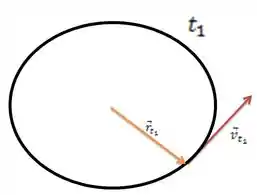
Passo 2
Mas se liga só, ele nos pede o módulo da aceleração centrípeta.
Lembra aí como se calcula? Saca só!
Mas quem seria o nosso
Justamente o módulo da velocidade nos dois casos, que nada mais nada menos é que:
Desta forma, teremos...
Passo 3
Mas pera aí! Ele não falou o , daí a conta não sai!
![]()
Calma! É só lembrar que, . Mas aí também temos que .
Daí, teremos que:
Mas e aí? Não temos o !
Aí que vem o pulo do gato!

Lembra dos vetores posição lá da nossa primeira figura. Dizendo que ele fez o percurso entre e , teremos o seguinte caso:
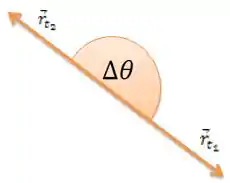
E o nosso será .
Passo 4
Assim, vamos ter que:
Agora, tacando lá na fórmula do Passo 2, teremos:
Passo 5
b)
Pela definição de aceleração média, teremos que:
Calculando o módulo da aceleração, teremos:
Resposta
a)
b)
Exercício Resolvido #4
Elaboraação Própria
Uma formiga pula em uma roda gigante que está descrevendo um movimento circular uniforme de Raio valendo 2m. No instante a velocidade da formiga é , medida em um sistema de coordenadas horizontal. No instante a velocidade é Calcule a aceleração centrípeta e a aceleração média da formiga no intervalo de tempo , que é menor que um período.
Passo 1
Vamos lá, galera!
Como ele nos diz que temos um MCU, no tempo e no tempo teremos as velocidades e o vetor posição , como mostrado abaixo.
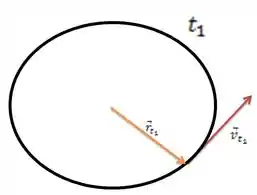
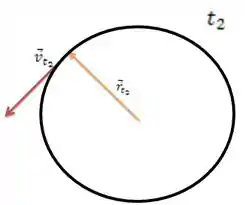
E a gente pode calcular a aceleração centrípeta assim, né:
Mas quem seria o nosso
Justamente o módulo da velocidade nos dois casos, que nada mais nada menos é que:
Desta forma, teremos...
Passo 2
Pela definição de aceleração média, teremos que:
Calculando o módulo da aceleração, teremos:
Resposta
a)
b)
Exercício Resolvido #5
Elaboração própria
Uma partícula descreve um movimento circular de raio 5m, com velocidade de módulo constante e igual a . Num intervalo de tempo 10 segundos, a partícula anda da circunferência. O módulo de seu vetor velocidade média é igual a
Passo 1
Os dados do enunciado são
O vetor velocidade média é
Vamos fazer um esboço do movimento, considerando o raio do movimento .
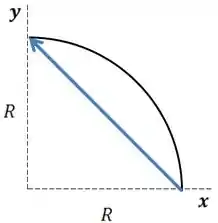
Vamos considerar que o corpo está girando no sentido anti-horário.
Passo 2
O vetor em azul, é o vetor deslocamento, como ele quer o módulo do vetor velocidade média devemos ter o módulo do vetor deslocamento.
Passo 3
Então
Prontooo!
Resposta
Letra E
Exercício Resolvido #6
UFRJ Física 1 P1 2012.1
Uma partícula descreve um movimento circular, com velocidade de módulo constante e igual a . Num intervalo de tempo em que percorre da circunferência, o módulo de seu vetor velocidade média é igual a
Passo 1
Os dados do enunciado são
O vetor velocidade média é
Vamos fazer um esboço do movimento, considerando o raio do movimento .
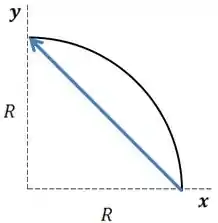
Vamos considerar que o corpo está girando no sentido anti-horário.
Passo 2
O vetor em azul, é o vetor deslocamento, como ele quer o módulo do vetor velocidade média devemos ter o módulo do vetor deslocamento.
Passo 3
Então
Porém, não temos nenhuma dessas variáveis.
Passo 4
Sabemos que o módulo da velocidade é ,
Como a velocidade é constante
Onde é a distancia percorrida, que nesse caso é do comprimento do círculo de raio .
O comprimento de um circulo completo é então
Passo 5
No módulo do vetor velocidade média temos , então vamos achar essa razão em função de .
Passo 6
Substituindo na equação do módulo da velocidade média
Resposta
Letra A
Exercício Resolvido #7
Cinemática Tridimensional
Considere as seguintes afirmações sobre os vetores velocidade e aceleração de um corpo em movimento:
A velocidade pode ser zero e a aceleração ser diferente de zero.
O módulo do vetor velocidade pode ser constante, com o vetor velocidade mudando com o tempo.
O vetor velocidade pode ser constante mas seu módulo variar com o tempo.
O vetor velocidade pode mudar de sentido com o tempo mesmo que o vetor aceleração permaneça constante.
São verdadeiras as afirmações:
- Todas as afirmações
- I, II e III
- II e III
- I, II e IV
- Nenhuma das afirmações anteriores.
Passo 1
Vamos analisar cada afirmação.
Verdadeiro, Basta lembrarmos do lançamento vertical para cima, onde a velocidade na altura máxima e zero, porém a aceleração da gravidade ainda está atuando;
Passo 2
Verdadeiro, no movimento circular uniforme é exatamente isso que acontece, temos a aceleração centrípeta mudando o vetor velocidade, no caso variando sua direção, mas o seu módulo permanece constante.
Passo 3
Falso, para o vetor ser constante ele precisa manter seu módulo constante.
Passo 4
Verdadeiro, é o que acontece no lançamento vertical para cima, a aceleração é constante, porem durante uma parte do movimento ele está com um sentido e em outra parte está com outro.
Resposta
Letra D
Exercício Resolvido #8
Halliday 9ª edição vol.1 cap.10 seção 2 questão 5
Um mergulhador realiza giros ao saltar de uma plataforma de metros. Supondo que a velocidade vertical inicial seja nula, determine a velocidade angular média do mergulhador.
Passo 1
Então, de acordo com as equações do movimento uniformemente acelerado, o tempo que o mergulhador leva para chegar à água é :
Nesse caso, de acordo com a equação da velocidade angular média, temos: