Movimento Retilíneo + Movimento Circular
Teoria
Agora, estudaremos situações em que o movimento de uma partícula é composto por movimento curvilíneo e movimento retilíneo.
Fica tranquilo! Se você aprendeu bem cada um desses movimentos, você vai ver que é só aplicar os conceitos aprendidos anteriormente.
Um exemplo disso é girar uma bolinha sobre a mesa, presa por uma corda mas em um determinado momento a corda se rompe, fazendo com que a bolinha seja lançada horizontalmente pra fora da mesa.
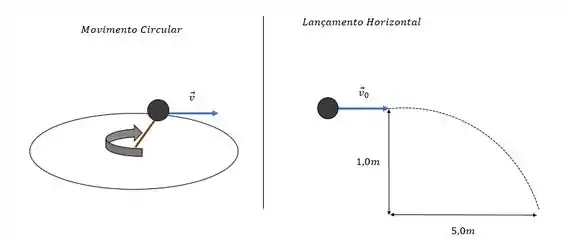
Enquanto a bolinha gira, ocorre um movimento circular. Então, todas as equações do movimento circular apresentadas nas teorias anteriores são válidas.
Quando a bolinha se solta acontece um lançamento horizontal.
O importante é sabermos a velocidade no momento em que a bolinha se solta, pois aplicaremos uma equação da cinemática. Podemos descobrir a velocidade nesse momento por meio da fórmula que estudamos:
Bora imaginar aquela bolinha ali, fazendo um movimento circular na mesa com 2,0 metros de raio localizada á 1,0 metro do chão. Se a corda se romper a bolinha será lançada a 5 metros de distância, como calcular a aceleração centrípeta desse movimento?
Vamos fazer um desenho pra analisar o que acontece quando a bolinha se desprende.
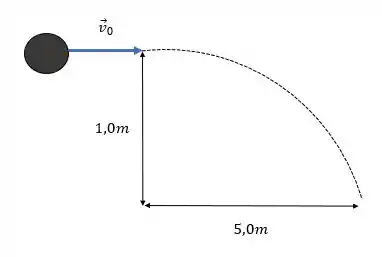
Temos um lançamento horizontal, e lembrando que nesses casos a velocidade horizontal permanece constante ao longo do movimento e que a velocidade inicial é apenas na horizontal.
Como na horizontal não teremos variação da velocidade, temos um Movimento Uniforme, e sabemos o alcance total desse movimento:
Mas e aí? Precisamos do tempo de queda e a gente vai tirar ele da parte vertical, onde temos um Movimento Uniformemente Variado:
Como não possui velocidade inicial em a gente elimina o termo com :
E essa bolinha saiu da posição e chegou no solo, onde , logo:
Resolvendo para encontrar , teremos:
Calculando a velocidade então:
Por fim a gente tem:
Onde essa velocidade do movimento circular é a mesma velocidade inicial que iniciou o lançamento horizontal, ou seja, aquele que acabamos de calcular.
E é isso que a gente precisa saber sobre essa combinação de movimentos! Bora praticar?
Exercícios Resolvidos
Exercício Resolvido #1
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 1 , 8º ed. Rio de Janeiro: LTC , 2008, pp 89-67.
Um menino faz uma pedra descrever uma circunferência horizontal com 1,5m de raio 2,0m acima do chão. A corda se parte e a pedra é arremessada horizontalmente, chegando ao solo depois de percorrer uma distância horizontal de 10m. Qual era o módulo da aceleração centrípeta da pedra durante o movimento circular?
Passo 1
Nessa questão é preciso analisar o movimento circular e o movimento oblíquo, após o rompimento da corda.
Para sabermos a aceleração centrípeta, precisamos descobrir a velocidade.
A figura abaixo mostra a trajetória da pedra após o rompimento da corda.
Passo 2
Sabemos do movimento do projétil que
Pela figura que montamos, vemos que quando a pedra chega ao solo, x vale e y vale .
Além disso, e a velocidade da pedra antes da ruptura é igual a .
Passo 3
Substituindo a equação de y para descobrirmos o tempo:
Passo 4
Substituindo a equação de x para descobrirmos a velocidade:
Passo 5
Como descobrimos a velocidade e sabemos o raio, basta substituir na fórmula:
Resposta
Exercício Resolvido #2
Elaboração Própria
Uma criança em um carrossel que realiza um movimento circular uniforme com 3,0m de raio e 1,25m acima do chão lança horizontalmente (com velocidade inicial na vertical sendo nula) um brinquedo que estava em sua mão para fora do carrossel, chegando ao solo depois de percorrer uma distância horizontal de 20m. Qual era o módulo da aceleração centrípeta da pedra durante o movimento circular?
Considere
Passo 1
Aqui a gente tem a mesma idéia da questão anterior!
Para sabermos a aceleração centrípeta, precisamos descobrir a velocidade.
Do movimento do brinquedo, no eixo x sendo um MU e no eixo y sendo um MUV, temos:
E pelos dados do proble,a vemos que quando o brinquedo chega ao solo, x vale e y vale . Além disso, e a velocidade do brinquedo no começo do movimento a é igual a .
Passo 2
Substituindo a equação de y para descobrirmos o tempo:
Passo 3
E agora que temos o tempo, podemos substituir na equação de x para descobrirmos a velocidade:
Brinquedinho rápido, né não? :p
Passo 4
Como descobrimos a velocidade e sabemos o raio, basta substituir na fórmula:
Resposta
Exercício Resolvido #3
Elaboração Própria
Um ioiô faz uma trajetória circular de raio 1m com aceleração centrípeta de A corda do ioiô se rompe e ele é arremessado horizontalmente, chegando ao solo depois de percorrer uma distância horizontal de 24m. Qual foi o tempo de vôo do ioiô e a altura em que ela foi lançada?
Considere
Passo 1
Primeiro vamos analisar o nosso movimento! Temos algo assim:
Como a gente sabe, num lançamento horizontal a gente tem que seu movimento varia do eixo x pro eixo y, então:
Através da aceleração centrípeta podemos descobrir o valor da velocidade em x, com isso podemos descobrir o tempo de vôo e consequentemente descobrir a altura que o ioiô foi lançado!
Passo 2
Vamo lá, como sabemos:
Que é exatamente a velocidade de lançamento .
Passo 3
Como no eixo x a velocidade é constante, temos um UM (Movimento Uniforme), ficamos com a equação que mostramos lá em cima, então:
A distância percorrida foi de 24 metros, temos que
Então esse é o tempo de vôo do nosso ioiô!
Passo 4
Para descobrirmos a altura, sabendo que o lançamento foi horizontal (sem velocidade inicial no eixo y), temos que:
Prontooo! Terminamos, conseguimos! Esse ioiô aí pulou alto, ein? :p
Resposta
e
Exercício Resolvido #4
Elaboração Própria
Uma partícula faz uma trajetória circular de raio 5m com aceleração centrípeta de Imediatamente ao sair do movimento circular, essa partícula é arremessada horizontalmente, chegando ao solo depois de percorrer uma distância horizontal de 63m. Qual foi o tempo de vôo da partícula e a altura em que ela foi lançada?
Considere
Passo 1
Primeiro vamos analisar o nosso movimento! Temos algo assim:
Como a gente sabe, num lançamento horizontal a gente tem que seu movimento varia do eixo x pro eixo y, então:
Através da aceleração centrípeta podemos descobrir o valor da velocidade em x, com isso podemos descobrir o tempo de vôo e consequentemente descobrir a altura da partícula.
Passo 2
Vamo lá, como sabemos:
Que é exatamente a velocidade de lançamento .
Passo 3
Como no eixo x a velocidade é constante, temos um MU, ficamos com a equação que mostramos lá em cima, então:
A distância percorrida foi de 24 metros, temos que
Então esse é o tempo de vôo do nosso ioiô!
Passo 4
Para descobrirmos a altura, sabendo que o lançamento foi horizontal (sem velocidade inicial no eixo y), temos que:
Prontooo! Terminamos, conseguimos!
Resposta
e
Exercício Resolvido #5
Elaboração Própria
Em um jogo olímpico, um atleta em cima de um prédio lança um disco fazendo uma trajetória circular de raio 2m com velocidade tangencial a trajetória de 4m/s. Calcule a aceleração centrípeta do disco, a distância horizontal que o disco alcançou e a altura que o atleta lançou o disco sabendo que o tempo de vôo do disco foi de 2s.
Considere
Passo 1
Pra calcular a aceleração centrípeta, vamos usar aquela fórmulinha, lembra?
Passo 2
Como a gente sabe, num lançamento horizontal a gente tem que seu movimento varia do eixo x pro eixo y, então:
Como a velocidade da aceleração centrípeta é a própria e a questão nos deu o tempo do movimento, temos que:
Então essa é nossa distância horizontal. Show de bolinhas!
Passo 3
Para descobrirmos a altura, sabendo que o lançamento foi horizontal (sem velocidade inicial no eixo y), temos que:
Prontooo! Terminamos, conseguimos! E
Resposta
Exercício Resolvido #6
Elaboração Própria
Uma parícula que realizava uma trajetória circular de raio 5m com velocidade tangencial a trajetória de 20m/s é lançada horizontalmente ao fim desse movimento. Calcule a aceleração centrípeta e a distância horizontal da partícula sabendo que o seu tempo de vôo foi 10s. Considere
Passo 1
Pra calcular a aceleração centrípeta, vamos usar aquela fórmulinha, lembra?
Passo 2
Como a gente sabe, num lançamento horizontal a gente tem que seu movimento varia do eixo x pro eixo y, então:
Como a velocidade da aceleração centrípeta é a própria e a questão nos deu o tempo do movimento, temos que:
Então essa é nossa distância horizontal. Show de bolinhas!