Lançamento Vertical
Teoria
O lançamento vertical é um caso especial do Movimento Retilíneo Uniformemente Variado. Nele temos um movimento na vertical, na prática isso quer dizer que a sua aceleração vai ser igual a aceleração da gravidade.
Existem 3 tipos de lançamento vertical:
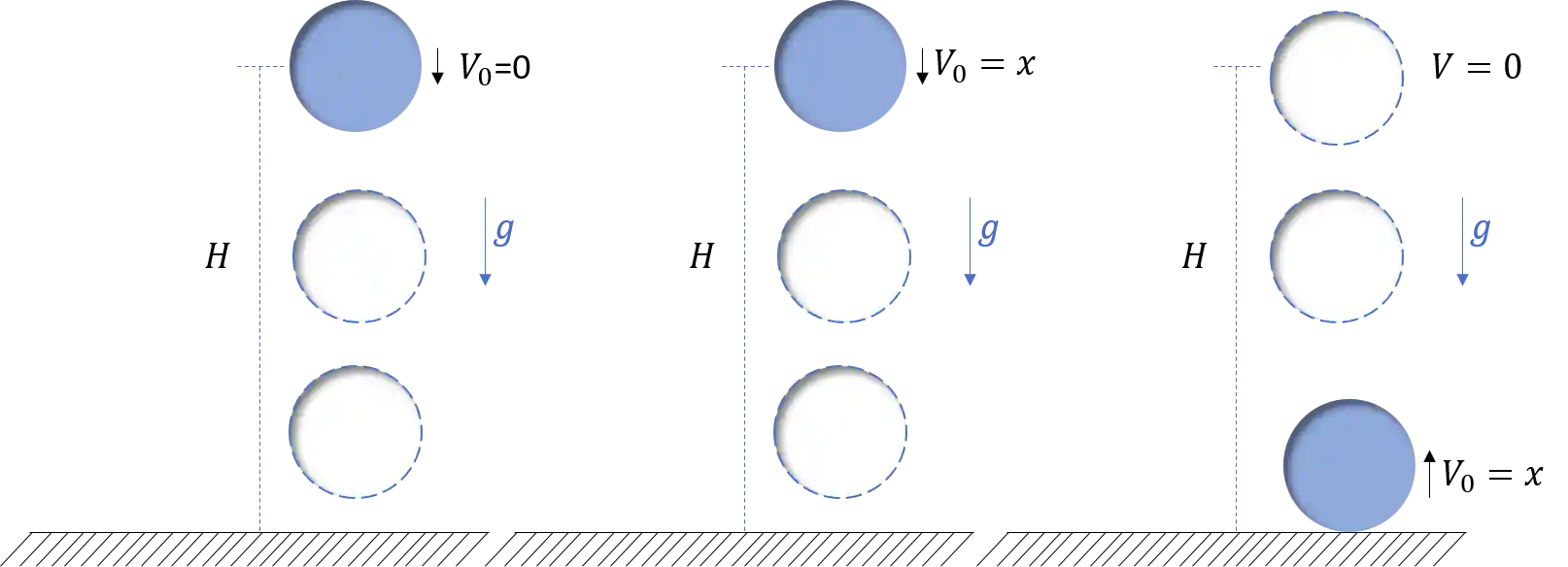
Na figura acima, podemos ver os 3 tipos de lançamento vertical! Mas agora vamos dar nome aos bois:
- Queda Livre: É o caso que a velocidade inicial
é igual a zero - Lançamento para baixo: É o caso que a velocidade inicial é para baixo, ou seja, ela NEGATIVA.
- Lançamento para cima: É o caso que a velocidade inicial é para cima, ou seja, ela é POSITIVA.
Se liga nesse resumo em vídeo que o Responde Aí preparou especialmente pra você, com tudo o que você precisa saber sobre Lançamento Vertical:
Ou então, continua comigo no textinho! 😉
Fórmulas do Lançamento Vertical
As fórmulas que vamos usar no lançamento vertical, são aquelas do MRUV, só que com algumas adaptações!
São elas:
- Equação da Velocidade:
- Equação da Posição:
- Equação de Torricelli:
Onde:
é o tempo, em ; é a velocidade do objeto, no tempo , em ; é a velocidade inicial, em ; é a altura do objeto, no tempo , em é a altura inicial do objeto, em ; é a aceleração da gravidade, em .
Lançamento Vertical para cima
Quando alguém lança um objeto verticalmente para cima com uma velocidade inicial
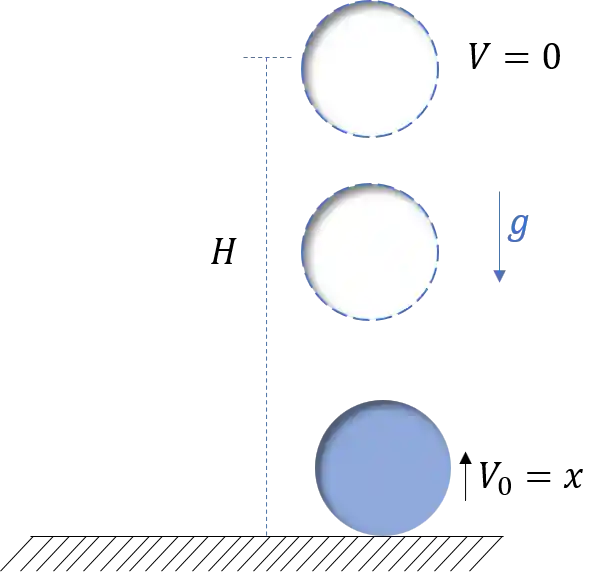
A altura máxima atingida por esse objeto é quando ele para
Outro detalhe importante é que o tempo de subida é igual ao tempo de descida, então se um objeto gastou
Podemos calcular o tempo de subida, fazendo:
Queda Livre e Lançamento Vertical para baixo
A diferença entre queda livre e o lançamento vertical para baixo é só a velocidade inicial! Na queda livre ela é nula, enquanto no lançamento para baixo ela é negativa!
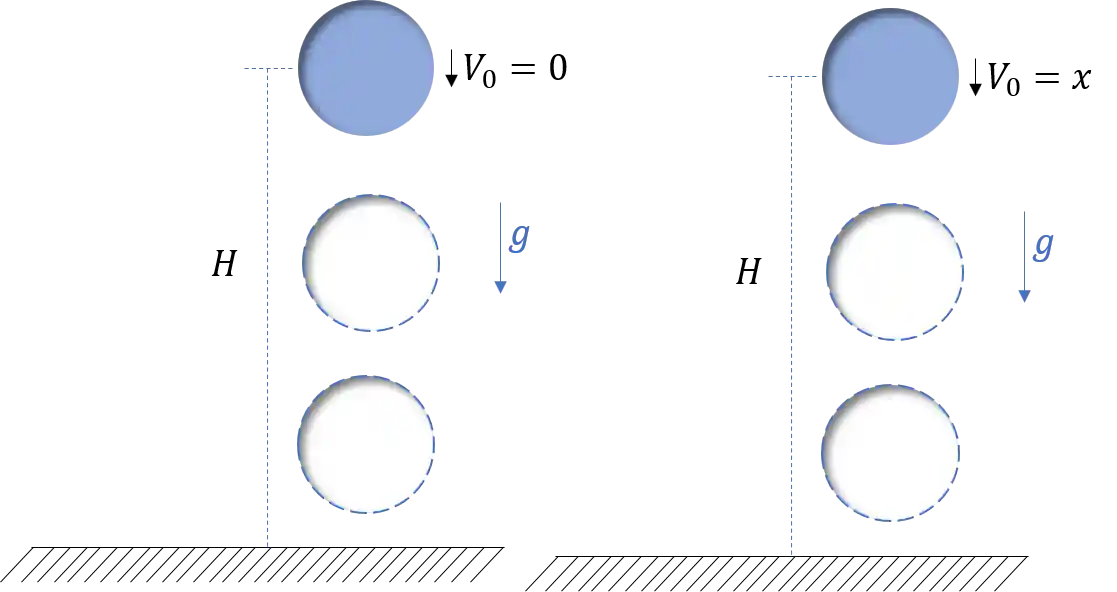
Vamos ver um exemplo de lançamento para ficar mais claro!
Queda Livre: Exemplo
Uma bolinha é largada de uma altura de
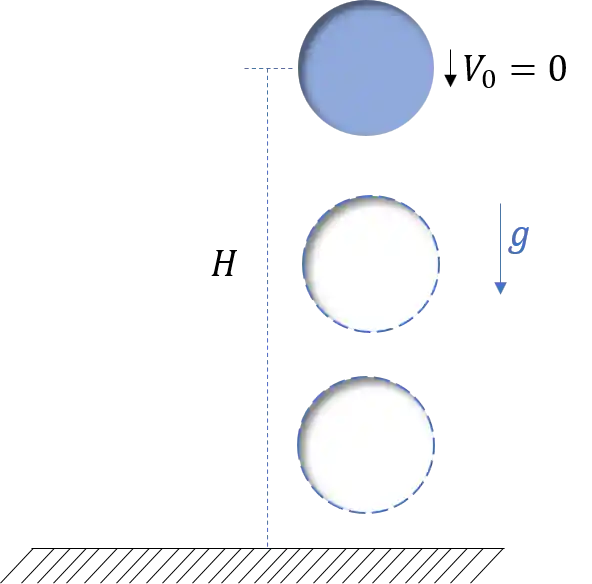
A bolinha que foi “abandonada” de uma certa altura, a velocidade inicial então vai ser zero. Isso quer dizer que ela está em queda livre!
Como a altura que ela é “abandonada” é
Lembra que tudo que aponta para baixo é negativo? Então, a gravidade aponta para baixo certo? Ou seja, ela é negativa.
O problema pede o tempo que a bolinha vai atingir o chão. Atingir o chão quer dizer que a posição da bolinha no momento que ela chega no chão é zero.
Como ele quer o tempo e temos a posição, vamos usar a equação da posição pelo tempo.
Substituindo:
Resolvendo:
A bolinha demora
Agora que aprendemos lançamento vertical, bora partir para os exercícios para dominar bem essa matéria?!
Fórmulas do Lançamento Vertical
Queda Livre e Lançamento Vertical para baixo
Exercícios Resolvidos
Exercício Resolvido #1
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 36 - Modificado
Um tijolo é largado (velocidade inicial nula) do alto de um edifício. Ele atinge o solo em . A resistência do ar pode ser desprezada, de modo que o tijolo está em queda livre. a) qual é a altura do edifício? b) qual o módulo da velocidade quando ele atinge o solo?
Dado:
Passo 1
O movimento da queda do tijolo, como foi dito no enunciado é queda livre, podemos tirar do enunciado os seguintes dados,
Estamos considerando que o espaço inicial () é a altura H em que ele estava antes do movimento de queda livre e que ele vai atingir o solo no espaço final, por isso .
Passo 2
Como o sentido positivo é para cima (sentido que sempre adotaremos no lançamento vertical), e ele é solto do alto do edifício podemos considerar que durante o movimento de queda ele vai “perder espaço” até alcançar o solo, por isso consideramos sua aceleração da gravidade como negativa.
Ele deu o tempo e queremos a posição inicial, então vamos usar a equação da posição pelo tempo
Passo 3
Agora ele quer a velocidade quando chega no chão, então vamos usar a equação da velocidade pelo tempo. Aqui também vamos considerar a gravidade negativa, porque aponta no sentido contrário do eixo vertical.
Como ele pede o módulo consideramos a velocidade sem o sinal.
Obs: O sinal negativo mostra o sentido para baixo.
Resposta
Exercício Resolvido #2
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 1 , 8º ed. Rio de Janeiro: LTC , 2008, pp 40-99
Um certo malabarista normalmente arremessa bolas verticalmente até uma altura . A que altura as bolas devem ser arremessadas para passarem o dobro do tempo no ar?
Passo 1
É um problema de lançamento vertical. Podemos considerar que o tempo de subida é igual ao tempo de descida, então se considerarmos que a bola gasta segundos para chegar até a altura , podemos dizer que para subir e descer segundos, certo?
O problema quer saber qual a altura para que o tempo de vôo seja o dobro, ou seja, . Com um tempo total de teríamos de subida e de descida.
Mas como sabemos estamos tratando de um movimento vertical, ou seja, o objeto primeiramente realiza um movimento de subida e em seguida muda o sentido do seu movimento e inicia o movimento de descida.
Passo 2
Para o cálculo da altura máxima só nos interessa parte do movimento, pode ser a subida ou a descida das bolas. Aqui usaremos as equações do lançamento vertical para cima, que considera o tempo de subida, e nesse caso a equação da altura fica desse jeito:
O sinal de é negativo pois é oposto ao movimento aqui.
E pra encontrar a velocidade inicial da bolinha podemos usar o seguinte:
No ponto da altura máxima temos e portanto conheceremos o valor de .
Tomando que é o ponto do solo e substituindo teremos a seguinte equação pra altura.
Passo 3
Com a equação da altura máxima calcularemos a altura para o tempo normal, e a altura para o dobro do tempo.
Para o tempo dobrado temos:
Agora é só dividir por e teremos a relação das alturas:
Resposta
As bolas devem ser arremessada a uma altura 4 vezes maior que a altura inicial.
Exercício Resolvido #3
PUC 2008
Uma bola é lançada verticalmente para cima, a partir do solo, e atinge uma altura máxima de 20 m. Considerando a aceleração da gravidade g = 10 m/s², a velocidade inicial de lançamento e o tempo de subida da bola são:
a) 10 m/s e 1s
b) 20 m/s e 2s
c) 30 m/s e 3s
d) 40 m/s e 4s
e) 50 m/s e 5s
Passo 1
Como a altura máxima da bola é de 20m e a gente sabe que na altura máxima a velocidade da bola é 0, temos que:
Show!
Passo 2
Agora que temos a velocidade inicial da bola fica fácil calcularmos o tempo de subida, né? É só lembrar de novo que a velocidade na altura máxima é 0! Então, temos:
Lindooooo!
Resposta
b) 20 m/s e 2s
Exercício Resolvido #4
BrasilEscola
Um móvel é atirado verticalmente para cima a partir do solo, com velocidade de 72 km/h. Determine:
a) as funções horárias do movimento;b) o tempo de subida;c) a altura máxima atingida;d) em t = 3 s, a altura e o sentido do movimento;e) o instante e a velocidade quando o móvel atinge o solo.
Obs.: Adote g = 10m/s²
Passo 1
Bom, vamo nessa! Temos um movimento uniforme variado devido a presença da aceleração da gravidade, certo? Então nossa função horária do espaço é dada por:
E a função horária da velocidade:
Aqui a gente precisa tomar cuidado com o SI! A velocidade inicial foi dada em e precisamos converte-la para , fazendo:
Como temos a velocidade inicial (20m/s) e a gravidade (10m/s²) que é contrária ao movimento (então o sinal é negativo), é só substituir!
Show!
Passo 2
Na letra b a gente quer saber o tempo de subida, e pra gente calcular isso é só a gente lembrar que na altura máxima a velocidade é 0! Então é só usarmos a função da velocidade que achamos na letra A, assim ó:
Lindu dimai!
Passo 3
Bom, e pra gente descobrir a altura máxima? A gente tem o tempo que o móvel chegou a altura máxima e temos a equação do espaço! É só jogar na fórmulinha, né? Bó lá!
Bouaaaaa!
Passo 4
Pra gente descobrir a altura no tempo de 3 segundos... É só substituir na fórmula que nem fizemos com o 2! Bora lá:
E o sentido do movimento vai ser pra baixo, certo? Porque como a altura máxima é no tempo de 2, quando a partícula chega nesse tempo ela retorna o movimento, né?
Então fechouuu!
Passo 5
O tempo de descida é igual ao tempo de subida, lembra? Então o móvel irá atingir o solo novamente depois de 4s, que é 2s de subida e 2s de descida! :D
A velocidado com que o móvel retorna ao solo é a mesma com que ele foi lançado, assim V = 72 km/h.
Resposta
a) e
b) 2s
c) 20m
d) 15m
e) 4s e 72km/h
Exercício Resolvido #5
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 1 , 8º ed. Rio de Janeiro: LTC , 2008, pp 37-54
A figura mostra a velocidade em função da altura para uma bola lançada verticalmente para cima ao longo de um eixo . A distância é de . A velocidade na altura é . A velocidade na altura é Determine a velocidade
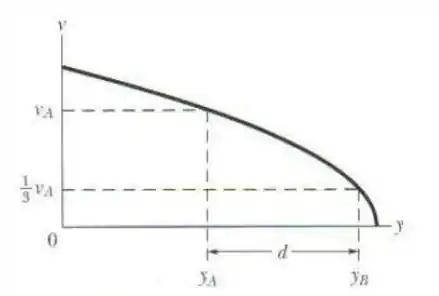
Passo 1
O problema trata de uma bola lançada para cima, como o tempo não foi dado nem pedido, vamos estudar o movimento usando a equação de torricelli, assim temos
Onde , e devido ao sentido adotado no lançamento vertical.
Passo 2
Para achar o valor de , basta substituir o valor de e isolar a velocidade
Resposta
Exercício Resolvido #6
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 54 – Modificado
Um balonista de ar quente se desloca verticalmente para cima com velocidade constante de módulo igual a deixa cair um saco de areia no momento em que ele está a uma distância de acima do solo.
Depois que ele é largado, o saco de areia passa a se mover em queda livre.
Calcule a posição e a velocidade do saco de areia e depois que ele é largado.
Calcule o tempo que o saco de areia leva para atingir o solo desde o momento que ele foi lançado.
Qual é a velocidade do saco de areia quando ele atinge o solo?
Qual a altura máxima, em relação ao solo, atingida pelo saco de areia?
Passo 1
Quando ele larga o saco de areia, como o balão está subindo com velocidade , o saco de areia inicialmente terá essa mesma velocidade, nesse mesmo sentido.
Isso pode parecer estranho, já que o corpo foi largado, mas vamos lembrar que pela Lei da Inércia “um corpo que está se movendo tende a continuar em movimento, até que a resultante das forças atuando sobre ele não seja nula”. Lembra o que acontece quando alguém freia bruscamente, e o carona é arremessado pra frente? Logo, o saco tende a continuar subindo a , porém a gravidade vai começar a atuar sobre ele, retardando o movimento de subida.
Então, ele faz um lançamento vertical para cima.
Além disso, ele é largado de de altura, sendo essa sua posição inicial.
Passo 2
Ele quer a posição e a velocidade em um tempo dado, então basta usarmos as equações da posição pelo tempo e da velocidade pelo tempo.
Começando pela posição,
Para
Passo 3
Para
Passo 4
Vamos para a velocidade
Para
Passo 5
Para
Repare que a velocidade em é positiva, enquanto a velocidade em é negativa.
Isso quer dizer que no primeiro momento o saco de areia está subindo, e em seguida está descendo.
Passo 6
Para descobrir o tempo que ele chega ao solo, significa o tempo quando .
Vamos usar então a equação da posição pelo tempo.
Resolvendo a equação de 2º grau,
O tempo não é negativo, e por isso vamos ignorar quando ele for menor que zero.
TEMPO SEMPRE POSITIVO.
Passo 7
Ele quer a velocidade, podemos usar tanto a equação da velocidade pelo tempo, como a equação de Torricelli.
Neste caso como o valor do tempo é algo, levemente, ruim de fazer conta, afinal envolve um raiz não exata.
Vamos então usar a equação de Torricelli.
Encontramos duas respostas, como ele pede a velocidade é importante mostrar qual o sentido dela. Como ao chegar no chão o saco de areia estará CAINDO, sua velocidade é para baixo, logo negativa.
Passo 8
Como vamos achar a altura máxima?
Já vimos que a altura máxima é quando a velocidade é zero. Como ele não deu nem pede o tempo vamos usar a equação de Torricelli,
Resposta
Para
Para
Exercício Resolvido #7
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 1 , 8º ed. Rio de Janeiro: LTC , 2008, pp 40-105
Uma pedra é lançada verticalmente para cima. Durante a subida ela passa por um ponto A com velocidade e por um ponto , acima de , com velocidade Calcule a velocidade e a altura máxima alcançada pela pedra acima do ponto .
Passo 1
O problema pede para você estudar o lançamento para cima de uma pedra. Como não foi pedido nem dado o tempo vamos estudar esse movimento usando a equação de torricelli.
Onde , e devido ao sentido adotamos para lançamentos verticais.
Passo 2
Para achar a velocidade vamos reescrevendo a equação e substituindo as informações dada pelo enunciado temos
Como estamos analisando a subida, a velocidade é positiva pois o movimento está no sentido positivo.
Se substituirmos por , teremos :
Passo 3
Na altura máxima a velocidade final é zero. Assim temos que .
Como queremos calcular a altura em relação ao ponto B, temos que usar como velocidade inicial a velocidade nesse ponto, correto? No passo anterior vimos que a velocidade no ponto é e, pelo enunciado, sabemos que a velocidade em B é metade disso! Logo a nossa velocidade inicial será .
Agora é só usar a equação de Torricelli!
Resposta
Exercício Resolvido #8
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 58 – Modificado
Um excursionista atento vê uma pedra cair do alto de um morro vizinho e nota que ela leva para cair a última terça parte da sua trajetória até o solo. Despreze a resistência do ar.
Qual é a altura do morro em metros?
Passo 1
Como a pedra está caindo, conseguimos ver que ela está em uma queda livre. Essa informação é bem importante pois um corpo em queda livre não possui velocidade inicial.
O esquema do corpo é esse aqui:
A aceleração do corpo é a mesma da gravidade e queremos encontrar a altura e o enunciado também nos diz que ela percorre um terço da altura num tempo de 1,3s, seria esse esqueminha aqui:
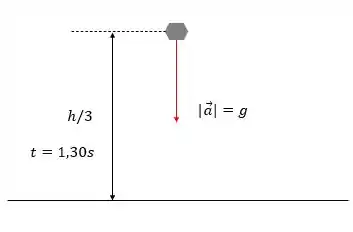
Nesse segundo momento temos um trecho de lançamento para baixo pois a pedra já adquiriu velocidade, precisaremos calcular essa velocidade e então aplicar a equação da altura nesse ponto onde .
Passo 2
A pedra começa em queda livre, mas no ponto da terça parte da altura já tem uma velocidade que deve ser considerada, podemos usar a equação de torricelli pra relacionar essa velocidade com a altura que temos aí:
Onde e já que o movimento começa em queda livre:
Essa velocidade é a velocidade para que usaremos como a velocidade do ponto inicial para .
Passo 3
A equação da altura a 2/3 de pode ser escrita como um lançamento pra baixo:
A variação de altura nesse ponto a gente já sabe é que usaremos nesse trecho, pra que a gente possa encontrar a partir disso o valor de
E aqui podemos substituir o tempo que foi medido
Resolvendo as continhas a equação vai ficar com essa cara:
Passo 4
Chatinho de resolver né? Vou te ensinar um macete pra sair desses casos sem precisar sair elevando um monte de gente ao quadrado, beleza? Vamos mudar as variáveis pra ajudar nas contas.
Daí nossa equação fica com essa cara:
Multiplicando geral por 3 e deixando tudo no mesmo lado a gente vai ter o seguinte:
E aqui é bháskara, sem pensar duas vezes.
Vamos apenas considerar o valor positivo de aqui pois estamos falando da raiz de uma medida espacial que deve também ser positiva.
Resposta