Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Energia Potencial Elástica

Ver Todos os Exercícios

Teoria

Além da energia potencial gravitacional, nós vamos trabalhar com outra energia potencial também, que é a elástica!!

Energia potencial associada a uma mola.

U e l = k Δ x 2 2

Lembrando que Δ x é o quanto a mola muda de tamanho e que não importa se a mola está sendo comprimida (reduzida de tamanho) ou esticada (aumentando de tamanho), o importante mesmo é o quanto ela está diferente do tamanho inicial.

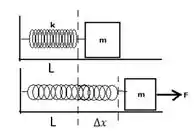
Aquele k ali é a constante elástica da mola. Esse k que vai dizer se é fácil ou não estica-la. Quanto maior for o k , mais difícil é esticar a mola.

Só lembrando aquela partezinha chata de SI ...

k = N m

Δ x = m

Alguns exercícios vão dar unidades diferentes, ai a gente sempre precisa manter esses padrões pra trabalharmos sempre com uma mesma unidade.

#PartiuPassar

Exercícios Resolvidos

Exercício Resolvido #1

TIPLER,P.- Física para Cientistas e Engenheiros, Vol 1,6ª Edição, LTC,2009., pp 231 – 23.

Uma mola tem uma constante de força 1,0   .   10 4 N / m   . De quanto esta mola deve ser esticada para que sua energia potencial seja igual a:

  1. 50   J
  2. 100   J

Passo 1

A energia potencial de uma mola é dada pela fórmula:

U s = k x 2 2

Sempre ficar atento nesses problemas que as unidades precisam sempre estar no SI.

Passo 2

Alternativa a)

k x 2 2 = U s

Isolando o x que é a incógnita do nosso problema temos:

x = 2 U s k

Substituindo os valores na expressão temos:

x =   2 ×   50 10 4 = 1 100 = 1 10

x = 0,1   m

Passo 3

Alternativa b)

k x 2 2 = U s

Isolando o x que é a incógnita do nosso problema temos:

x = 2 U s k

Substituindo os valores na expressão temos:

x =   2 × 100 10 4 = 2 100 = 2 10

x ≈ 0,14   m

Resposta

l e t r a   a )   0,10 m

l e t r a   b )   0,14 m

Exercícios de Livros Relacionados

15. Você precisa construir um dinamômetro para medir massas. Você deseja que cada 1,0c m de comprimento ao longo da escala corresponda a uma diferença de massa de100g . Qual deve ser o valor da consta
16. Uma mola de 10c m de comprimento é presa ao teto de uma casa. Quando uma massa de 2,0k g é suspensa por ela, a mola passa a ter o comprimento de 15c m . Qual é a constante elástica da mola? Qual s
14. Calçando sapatos com travas no solado, um corredor empurra um trenó de 20k g sobre o gelo sem atrito por meio de uma mola horizontal cuja constante elástica vale 150N / m . A mola está esticada 20
17. Uma massa de 5,0k g , suspensa por um dinamômetro, é gradualmente empurrada para baixo sobre uma mola vertical, como mostrado na FIGURA EX10.17. O dinamômetro marca o peso em newtons. Quanto marca
75. Como hobby, você gosta de participar de encenações de batalhas da Guerra Civil Norte-Americana. Os canhões daquela época eram “carregados pela boca”, no sentido de que uma carga de pólvora e uma b