Equilíbrio Estático em Barras Horizontais
Produzido por Ludovic BeghinTeoria
Introdução
A gente já tá sabendo como funciona o equilíbrio em diversos casos, mas e com as barras horizontais?
Para as barras horizontais não muda muita coisa, a gente continuará usando as equações de equilíbrio:
As barras devem sempre respeitar essas duas condições juntas e isso vai depender de alguns fatores como o comprimento da barra, distância até o apoio e pesos envolvidos nela.
Equilíbrio estático
Para a barra estar em equilíbrio ela não pode girar e tombar ou ter alguma força resultante sem alguém pra combater, vamos fazer um exemplo pra entender melhor.
Imagina a seguinte situação, a barra abaixo com comprimento indicado recebe um peso de massa na extremidade mostrada. Sabendo que a barra possui massa de , é possível que a barra esteja equilibrada se no lado esquerdo do apoio eu coloco um peso de ?
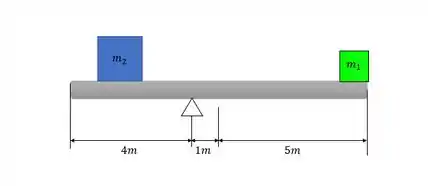
Essa resposta não é tão óbvia, a nossa intuição diria que não é possível equilibrar uma barra com pesos tão diferentes, mas precisamos analisar. A gente vai aplicar as duas equações mostradas na introdução e avaliar se é possível para a barra mostrada.
A primeira coisa a se fazer de tudo é desenhar o DCL indicando as forças, lembrando só que:
E não podemos esquecer do peso da barra, beleza?
Agora podemos indicar no DCL as forças:
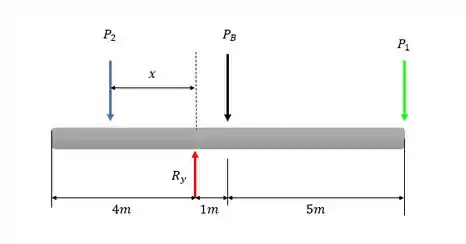
E quem é essa distância É a distância do bloco 2 que precisa ser menor que metros pra satisfazer a condição de equilíbrio, ou seja, precisa estar contida da barra.
Repare que no lugar do apoio apareceu a força que é a força que o apoio faz na barra para suportar as cargas. Outro detalhe é que o peso foi colocado no centro da barra, isso acontece, pois ela é homogênea que na nossa língua significa que é a massa da barra está distribuída uniformemente e nesses casos podemos considerar a massa total concentrada no seu centro.
Vamos aplicar a primeira equação de equilíbrio e aqui arbitrarei pra cima o sentido positivo:
E substituindo os valores:
Se a barra estivesse livre ela teria uma força resultante para baixo, mas o apoio combate essa resultante com a força .
Vamos agora ao maior problema pro equilíbrio da barra que são os torques. Presta muita atenção, o ponto que você escolhe é fundamental para facilitar as suas contas e você também deve arbitrar um sentido de giro. Lembrando que o torque relativo a qualquer ponto é dado por:
Onde é a força e é a distância perpendicular do ponto até a força.
Lembrando que pro equilíbrio ser verdade a condição deve ser respeitada:
Vamos analisar o sentido do giro pra gente não dar bobeira com o sinal. As forças á direita fazem a barra girar no sentido horário, saca só.
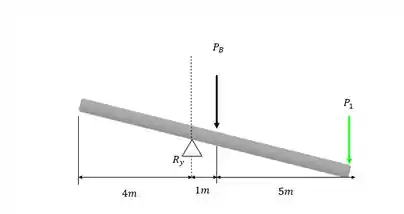
E a força da esquerda faz a barra girar no sentido anti-horário:
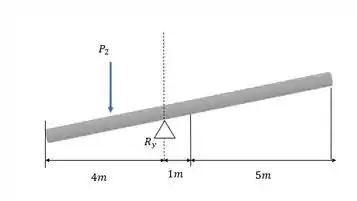
Aplicamos então o somatório dos torques no apoio, considerando anti-horário como o positivo.
Repara só! Para encontrar o valor de , eu não vou precisar do valor da força do apoio e isso aconteceu por que o eixo que eu escolhi foi exatamente aonde a força do apoio atuava, fazendo isso ela não aparece na conta.
Então, em uma questão desse tipo, você poderia ir direto para o somatório dos torques, fica a dica!
Substituindo:
Ou seja, se posicionarmos o bloco de massa a uma distância de do apoio, a barra estaria em equilíbrio. E se tivéssemos encontrado um valor maior que diríamos que é impossível colocar essa barra em equilíbrio, pois a massa estaria numa posição que não cabe na barra.
Geralmente os probleminhas desse tipo vão te pedir pra encontrar alguma distância, e aí é só seguir esse roteirinho que não tem erro. Partiu exercícios?