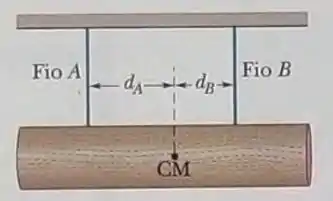
Na figura, um tronco homogêneo de está pendurado por dois fios de aço, e , ambos com de raio. Inicialmente, o fio tinha de comprimento e era mais curto do que o fio . O tronco agora está na horizontal. Qual é o módulo da força exercida sobre o tronco (a) pelo fio e (b) pelo fio ? (c) Qual é o valor da razão?
Passo 1
Fala galera, bora resolver essa parada?
Precisamos encontrar as reações em cada cabo, pra isso vamo ver o diagrama de corpo livre do tronco.
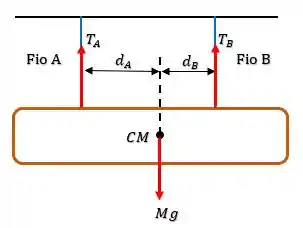
E se liguem, o tronco precisa estar em equilíbrio. Sendo assim:
Passo 2
Vamos considerar agora que inicialmente os fios e tinham um tamanho e e sofreram deslocamentos e nessa ordem. Sendo a diferença inicial entre os comprimentos e (tal que era mais longo que segundo o enunciado) e depois dos deslocamentos e adquirem comprimentos iguais, temos:
Agora, precisamos lembrar que, da definição de módulo de Young temos que a variação de comprimento de um corpo que se deforma em regime elástico é dado por:
Tal que , , e são a força à qual ele é submetido, seu comprimento, sua área transversal e seu Módulo de Young (note que esse módulo é análogo à constante elástica da Lei de Hooke). Usando essa expressão para e na última equação do passo 2, temos:
Passo 3
Vamos organizar a equação encontrada, isso vai ajudar a gente a substituir alguns valores.
Substituindo na equação acima, temos:
Colocando em evidência:
E enfim:
Tal que:
Lembrando que o módulo de elasticidade do aço pode ser considerado:
E também que media inicialmente 2,50m e o fio B possuía +2mm:
Passo 4
(b)Substituindo em , vem:
Passo 5
(c)Como o torque resultante é nulo devido à condição de equilíbrio do sistema, temos no centro do tronco e considerando o sentido horário positivo:
Então:
Resposta
(a)
(b)
(c)