Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 11.3 - Ex. 22
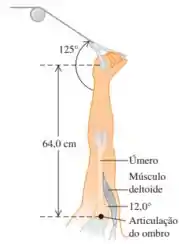
Você está fazendo exercícios em uma máquina Nautilus de uma academia, para fortalecer seus músculos do ombro (deltoides). Seus braços são levantados verticalmente e podem girar em torno da articulação do ombro, e você agarra o cabo da máquina em sua mão 64,0 cm a partir da articulação. O músculo deltoide está preso ao úmero a 15,0 cm da articulação do ombro e forma um ângulo de 12,0° com esse osso (Figura E11.22). Se você tiver preparado a tensão no cabo da máquina para 36,0 N em cada braço, qual é a tensão em cada deltoide se você simplesmente segurar seus braços esticados no lugar? (Dica: comece criando um diagrama do corpo livre do seu braço.)
Passo 1
E aii galera, vamos fazer mais uma questão? Bom... o enunciado nos dá a seguinte figura:
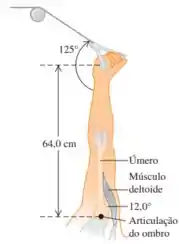
Queremos calcular a tensão em cada deltoide se alguém simplesmente segurar seus braços esticados no lugar se alguém tiver preparado a tensão no cabo da máquina para .
Para isso, temos que:
Onde é o torque, é força e é o tamanho do braço de alavanca.
Passo 2
O diagrama de corpo livre abaixo mostra as forças agindo no braço.
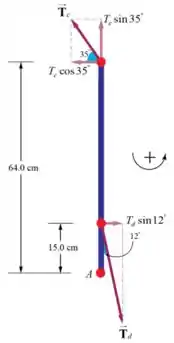
é a tensão no cabo e é a tensão no músculo deltóide.
Há também o peso gravitacional do braço e a força exercida pela articulação do ombro, mas eles não contribuem para o torque, então vamos ignorá-los em nosso digrama.
Passo 3
Deixando que as rotações no sentido anti-horário sejam positivas e aplicando a segunda condição para equilíbrio rotacional para o braço em torno de um eixo:
onde ( é o braço do momento de e é o braço do momento de .
Reorganize e resolvendo para
Resposta
A tensão no músculo deltóide é 605 N.