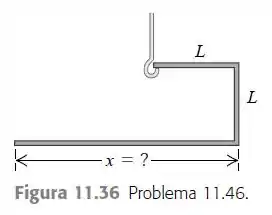
Uma barra de metal delgada e uniforme é dobrada em três segmentos perpendiculares, dois dos quais possuem comprimento L. Você deseja determinar qual deve ser o comprimento do terceiro segmento para que a unidade fique suspensa com dois segmentos horizontais, quando for sustentada por um gancho, como indica a Figura 11.36. Ache x e termos de L.

O centro de gravidade do objeto deve ter a mesma coordenada do gancho. Vamos usar a seguinte equação para localizar o centro de massa:

A massa de um segmento é proporcional ao seu comprimento. Defina como a massa por unidade de comprimento, então , onde é o comprimento de uma peça que possui massa .

Vamos utilizar as coordenas com a origem na borda direita do objeto e para a esquerda.

A massa de cada peça pode ser medida em seu centro de gravidade, que está em seu centro geométrico. Seja a horizontal peça de comprimento , seja a peça vertical de comprimento e peça horizontal de comprimento.