Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Padrões e Unidades

Ver Todos os Exercícios

Teoria

Fala, pessoal!

Aqui nós vamos falar um pouco sobre medições. Tipo, sabe quando nos pesamos ou medimos a nossa altura? Então, a altura e o peso são exemplos de grandezas físicas.

Como assim “grandezas físicas”?

Uma grandeza física é tudo que pode ser medido.

Mas como exatamente nós fazemos essas medições?

Vamos ver isso direitinho.

Unidades

Quando estamos medindo uma grandeza, sempre precisamos ter um padrão de referência. Como assim?

Por exemplo, imagina que eu te falo que vou andar 50 até a casa do meu primo. Se eu falar só isso, você vai ficar sem saber se se eu vou andar muito ou pouco.

Afinal, vou andar 50 o quê? Eu poderia querer dizer que vou andar 50 campos de futebol, 50 piscinas, 50 pés etc.

Ou seja: eu preciso explicitar uma unidade depois do número da medida e cada unidade apresenta um padrão de referência. Por exemplo, a unidade de comprimento pés, que eu mencionei acima, tinha como padrão de referência original o pé de um homem.

Agora, nós vamos ver algumas grandezas e suas unidades mais importantes.

Sistema Internacional de Unidades

Então, antigamente, cada cientista ou engenheiro usava as unidades que quisesse nos seus trabalhos. Imagina que zona! Toda vez que alguém fosse ler o trabalho de outra pessoa ia ter que ficar convertendo unidade para a que costuma usar... enfim, mó complicado né!

Aí, para facilitar, criaram o Sistema Internacional de Unidades (ou SI), que é utilizado para uniformizar as unidades de medida a serem usadas por todos, de forma a se adotar uma unidade para cada grandeza física chamada fundamental ou básica.

Quais são essas grandezas fundamentais e suas unidades no SI?

São essas 7 grandezas e 7 unidades que aparecem nessa tabela aqui:

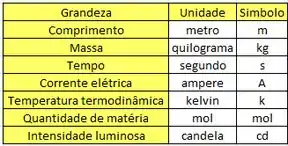
Como eu tinha falado antes, cada unidade apresenta um padrão de referência, que explica como ela é definida.

As definições das unidades básicas do SI vêm sofrendo adaptações ao longo dos anos.

Por exemplo, o segundo era definido inicialmente como o intervalo de tempo necessário para que um pêndulo de um metro de comprimento oscilasse de um lado para o outro.

Por serem difíceis de duplicar com exatidão, algumas definições foram substituídas por outras mais apuradas. Vamos ver algumas delas, mas não precisa decorar nada disso não heinnn!!! É só pra gente ter uma ideia melhor de como funciona =)

Padrões de Referência

Tempo

Como já falamos, o segundo já foi definido através de um pêndulo.

De 1889 até 1967, essa unidade de tempo era definida como certa fração do dia solar médio, a média de intervalos de tempo entre sucessivas observações do Sol em seu ponto mais elevado do céu.

O padrão atual, adotado em 1967, é muito mais preciso e é fundamentado em um relógio atômico de césio. Eu sei, bem louco, né.

Comprimento

Já a unidade de comprimento metro é definida como o tamanho do trajeto percorrido pela luz no vácuo durante um intervalo de tempo de 1/299 792 458 de segundo.

Massa

A unidade de massa quilograma, abreviada como k g , foi definida de 1960 até 2019 como a massa de um cilindro feito com uma liga de platina e irídio. Atualmente, essa unidade é baseada na constante de Planck.

Prefixos de Unidades

Agora já conhecemos as unidades das grandezas básicas do SI. A parada é que muitas vezes se usam prefixos pra modificar as unidades que nós acabamos de conhecer.

Mas, e aí, o que significam esses prefixos e como eles alteram essas unidades?

Relaxa e vem comigo que a gente vai desvendar esse mistério!

Vamos começar com um exemplo. O prefixo “quilo”, abreviado por k , representa sempre um múltiplo de 1000 , dessa forma aqui ó:

1   q u i l ô m e t r o = 1   k m = 1000   m e t r o s = 10 3   m

1   q u i l o g r a m a = 1 k g =   1000   g r a m a s = 10 3 g

1   q u i l o w a t t = 1 k W = 1000   w a t t s = 10 3   W

Vou te passar os prefixos mais comuns em cada unidade, e no final a gente passa uma tabela revisando tudo, fechou?

Comprimento

  1   n a n ô m e t r o = 1   n m = 10 - 9   m

1   m i c r ô m e t r o = 1   μ m = 10 - 6   m

1   m í l i m e t r o = 1   m m = 10 - 3   m

1   c e n t í m e t r o = 1   c m = 10 - 2   m

1   q u i l ô m e t r o = 1   k m = 10 3   m  

Massa

1   m i c r o g r a m a   = 1 μ g = 10 - 6   g = 10 - 9   k g

1   m i l i g r a m a = 1 m g = 10 - 3   g = 10 - 6   k g

1   g r a m a = 1   g = 10 - 3   k g

Tempo

1   n a n o s e g u n d o   = 1   n s = 10 - 9   s

1   m i c r o s e g u n d o = 1   μ s = 10 - 6   s

1   m i l i s e g u n d o = 1 m s = 10 - 3   s

Pronto!

Esses são os mais comuns. Mas também tem exercícios que pedem prefixos que vão aparecer na tabela seguinte. Não precisa ficar decorando todos antes de começar a praticar, ok? Fazendo os exercícios e consultando a tabela, eles vão ficando na cabeça sem você nem perceber!

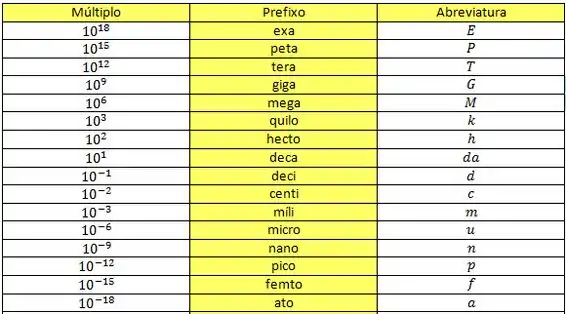
É isso, pessoal! Vamos pros exercícios!

Sistema Internacional de Unidades

Padrões de Referência

Prefixos de Unidades

Comprimento

Massa

Tempo

Exercícios Resolvidos

Exercício Resolvido #1

TIPLER,P. – Física para Cientistas e Engenheiros, Vol 1,6ª Edição, LTC,2009., pp. 22 – 1.

Qual das seguintes não é quantidade básica no sistema SI ?

  1. Massa
  2. Comprimento
  3. Energia
  4. Tempo
  5. Todas estas são quantidades básicas

Passo 1

Sabemos que são 7 as quantidades básicas no sistema SI. Olha o quadrinho aqui pra relembrar:

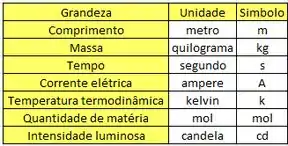
Passo 2

Alternativa (a) – Massa - Falsa

A massa faz parte do sistema SI, sendo o k g a unidade usada.

Passo 3

Alternativa (b) – Comprimento - Falsa

O comprimento faz parte do sistema SI, sendo o m   a unidade usada.

Passo 4

Alternativa (c) – Energia - Verdadeira

A energia não faz parte do sistema SI. Energia é um grandeza que relaciona massa, comprimento e tempo.

Passo 5

Alternativa (d) – Tempo - Falsa

O tempo faz parte do sistema SI, sendo o s a unidade usada.

Passo 6

Alternativa (e) – Todas são quantidades básicas - Falsa

A energia não é quantidade básica.

Resposta

Alternativa (c)

Exercício Resolvido #2

Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp. 27 – 1.7

Além de um pêndulo ou de um relógio de césio, que fenômeno físico poderia ser usado para definir um padrão de tempo ?

Passo 1

Meio viagem essa questão né.

Lembra do que eu falei lá na teoria? Algumas definições de unidades são alteradas por serem difíceis de duplicar com exatidão.

Assim, para definir um padrão de tempo é necessário algum fenômeno que seja periódico e seja fácil de duplicar com exatidão, vamos relembrar do pêndulo pra gente poder comparar com outras coisas.

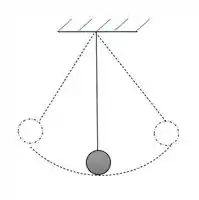
Se liga nesse movimento, quando o pendulo o faz por completo e volta pra posição inicial a gente diz que ele realizou uma oscilação completa e o tempo dessa oscilação é chamado de período que vai ser o mesmo para todas as oscilações. Como esse movimento é periódico a gente pode usar ele pra medir o tempo.

Passo 2

Lá na teoria a gente falou dos padrões de referência que já foram utilizados para criar unidades de tempo.

Um que vimos lá que pode ser utilizado é o dia solar médio, ou seja, a média dos intervalos entre sucessivas observações do sol no seu ponto médio, como na figura:

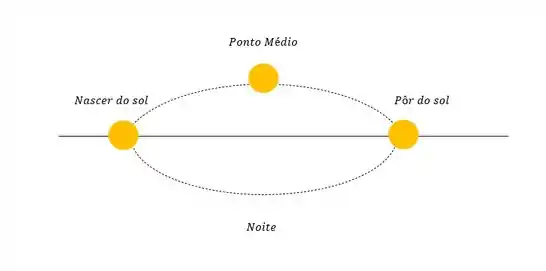
O tempo que o sol leva pra sair do ponto médio e voltar é um exemplo de fenômeno periódico, ainda que seja um grande período é uma forma de se medir o tempo.

Outro fenômeno que a gente poderia pensar em usar como definição de padrão de tempo é a ampulheta, saca só:

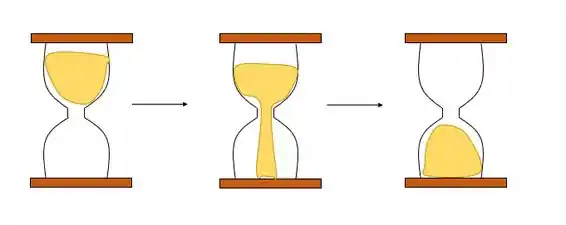
O processo da areia sair de um lado pra outro leva sempre o mesmo tempo, ou seja 1 período. E se virarmos a ampulheta esse processo vai se repetindo, por isso pode ser usado pra medir o tempo.

Diferente do sol, o exemplo da ampulheta geralmente serve pra medir um curto espaço de tempo.

Resposta

- Dia solar

- Ampulheta

Exercício Resolvido #3

Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp. 29 – 1.19. Modificado.

Um homem normal de meia idade vai ao hospital para fazer exames de rotina. A enfermeira anota a quantidade de 200 na sua ficha médica, mas esquece de incluir as unidades. Qual das seguintes grandezas esse número 200 pode representar?

  1. A massa dele em quilogramas
  2. A altura dele em metros
  3. A altura dele em centímetros
  4. A altura dele em milímetros
  5. A idade dele em meses

Dados: 1   m = 100   c e n t í m e t r o s   ( c m ) ; 1 m = 1000   m i l í m e t r o s   ( m m )

Passo 1

O homem que foi ao médico tem meia idade e é um homem normal, ou seja, nenhum dos números que a médica anotou podem fugir muito da normalidade.

Passo 2

Alternativa (a) – Falsa

Caso o peso dele fosse 200   k g , ele seria um homem com um peso muito acima da média.

Passo 3

Alternativa (b) – Falsa

Caso a altura dele fosse 200   m , o homem teria a mesma altura que um prédio com cerca de 60   andares.

Passo 4

Alternativa (c) – Verdadeira

Caso o número 200 represente a altura dele em centímetros, podemos pensar nessa altura em metros.

1   m = 100   c m

?   m = 200   c m  

Assim temos:

? m = 200   c m   x   1 m 100 c m

? m = 2 m

Assim teríamos um homem com 2   m . Um homem alto, mas essa altura acontece mais do que, por exemplo, um peso de 200   k g .

Passo 5

Alternativa (d) – Falsa

Caso o número 200 represente a altura dele em milímetros, podemos pensar nessa altura em metros.

1   m = 1000   m m

?   m = 200   m m  

Assim temos:

? m = 200   m m   x   1 m 1000 m m

? m = 0,2 m

Assim teríamos um homem com 0,2   m . Muuuuito baixo, né?

Passo 6

Alternativa (e) – Falsa

Caso o número 200 represente a idade dele em meses, podemos pensar nesse tempo em anos.

1   a n o = 12   m e s e s

?   a n o = 200   m e s e s  

Assim temos:

? a n o s = 200   m e s e s   x   1   a n o 12   m e s e s

? a n o s ≅ 16,6   a n o s

Assim teríamos um homem com 16,6   a n o s . Como ele não é adolescente, essa alternativa é falsa . :]

Resposta

Alternativa (c)

Exercício Resolvido #4

TIPLER,P. – Física para Cientistas e Engenheiros, Vol 1,6ª Edição, LTC,2009., pp. 23 –21.

Escreva, sem usar prefixos, o que se segue:

  1. 40   μ W
  2. 4   n s
  3. 3   M W
  4. 25   k m

Passo 1

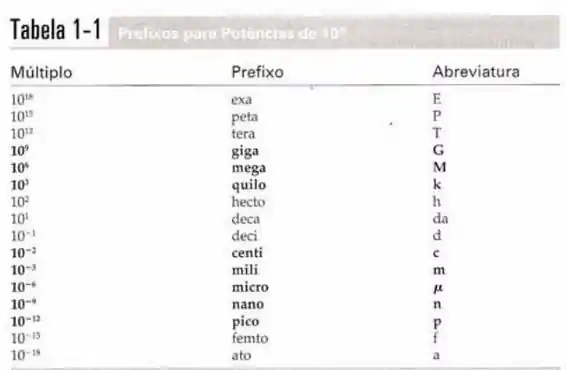
Observando os prefixos antes das unidades em cada alternativa, podemos calcular quanto cada abreviatura representa. Para consulta, vamos utilizar a tabela abaixo e substituir os valores.

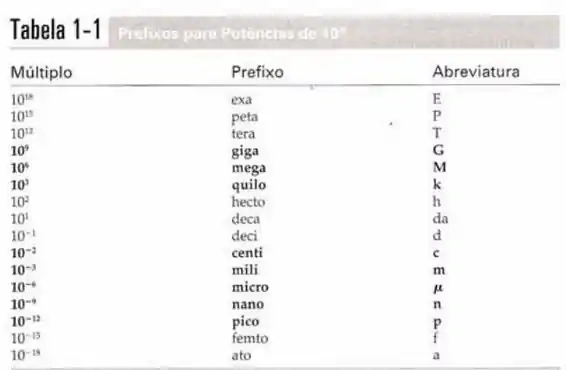
Passo 2

Alternativa (a) - 40   μ W

μ = 10 - 6

40   μ =   ?

? = 40 μ   x   10 - 6 μ

? = 0,00004

Logo temos que:

40   μ W = 0,00004   W

Passo 3

Alternativa (b) - 4   n s

n = 10 - 9

4   n =   ?

? = 4 n   x   10 - 9 n

? = 0,000000004

Logo temos que:

4   n s = 0,000000004   s

Passo 4

Alternativa (c) - 3   M W

M = 10 6

3   M =   ?

? = 3 M   x   10 6 M

? = 3000000

Logo temos que:

3 M W = 3000000   W

Passo 5

Alternativa (d) - 25   k m

k = 10 3

25   k =   ?

? = 25 k   x   10 3 k

? = 25000

Logo temos que:

25   k m = 25000   m

Resposta

Alternativa (a) - 0,00004   W

Alternativa (b) - 0,000000004   s

Alternativa (c) - 3000000   W

Alternativa (d) - 25000   m

Exercício Resolvido #5

TIPLER, Física, Vol 1,6ª Edição, LTC,2009., pp 23 – ex20

Escreva as quantidades seguintes, usando os prefixos listados na Tabela 1-1 e as abreviaturas listadas na tabela Abreviaturas para Unidades. Por exemplo, 10000 = 10   k m .

  1. 1000000   w a t t s
  2. 0,002   g r a m a
  3. 3   x   10 - 6   m e t r o
  4. 30000   s e g u n d o s

Passo 1

Observando os múltiplos dos prefixos percebemos que todos eles são potencias de 10 com múltiplos de 3 . O primeiro passo pra cada letra é escrever os algarismos em potenciais de 10 , depois, identificar a abreviatura e os prefixos indicados.

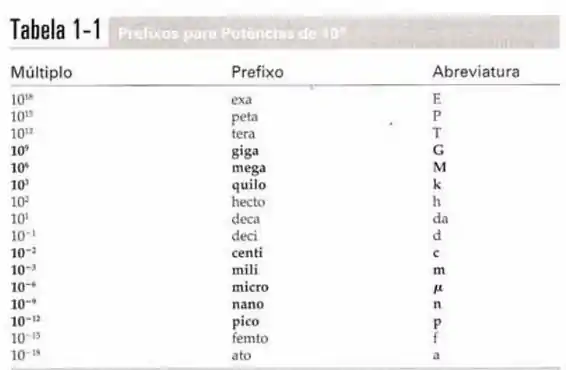
Passo 2

Alternativa (a) -   1000000   w a t t s

1000000   w a t t s = 10 6   w a t t s

10 6 = M

Logo temos:

1000000   w a t t s = 1   M W

Passo 3

Alternativa (b) - 0,002   g r a m a

0,002   g r a m a = 2   x   10 - 3   g r a m a s

10 - 3 = m

Logo temos:

0,002   g r a m a = 2   m g

Passo 4

Alternativa (c) - 3   x   10 - 6   m e t r o

Essa alternativa já simplificou o primeiro passo, pois o número já está escrito em potencias de 10

10 - 6 =   μ

Logo temos:

3   x   10 - 6   m e t r o = 3   μ m

Passo 5

Alternativa (d) - 3 0000   s e g u n d o s

30000 = 30   x   10 3

10 3 = k

Logo temos:

30000   s = 30   k s

Resposta

Alternativa (a) – 1   M W

Alternativa (b) – 2   m g

Alternativa (c) – 3   μ m

Alternativa (d) – 30   k s

Exercício Resolvido #6

TIPLER, Física, Vol 1,6ª Edição, LTC,2009., pp 23 – ex22

Escreva o que se segue (com ou sem unidade SI) usando prefixos (mas não suas abreviaturas). Por exemplo, 10 3   m e t r o s = 1   q u i l ô m e t r o .

  1. 10 - 12   v a i a
  2. 10 9   b a i x o
  3. 10 - 6   f o n e
  4. 10 - 18   m e n i n o
  5. 10 6   f o n e
  6. 10 - 9   b o d e
  7. 10 12   t o u r o

Passo 1

O primeiro passo em cada alternativa é identificar os prefixos usando a tabela de unidades.

Passo 2

Alternativa a) 10 - 12   v a i a

10 - 12 = p i c o

Logo temos:

10 - 12   v a i a = p i c o v a i a

Passo 3

Alternativa b) 10 9 b a i x o

10 9 = g i g a

Logo temos:

10 9 b a i x o = g i g a b a i x o

Passo 4

Alternativa c) 10 - 6   f o n e

10 - 6 = m i c r o

Logo temos:

10 - 6 f o n e = m i c r o f o n e

Passo 5

Alternativa d) 10 - 18   m e n i n o

10 - 18 = a t o

Logo temos:

10 - 18 m e n i n o = a t o m e n i n o

Passo 6

Alternativa e) 10 6   f o n e

10 6 = m e g a

Logo temos:

10 6   f o n e = m e g a f o n e

Passo 7

Alternativa f) 10 - 9   b o d e

10 - 9 = n a n o

Logo temos:

10 - 9 = n a n o b o d e

Passo 8

Alternativa g) 10 12   t o u r o

10 12 = t e r a

Logo temos:

10 12   t o u r o = t e r a t o u r o

Resposta

Alternativa (a) - p i c o v a i a  

Alternativa (b) - g i g a b a i x o  

Alternativa (c) - m i c r o f o n e  

Alternativa (d) - a t o m e n i n o  

Alternativa (e) - m e g a f o n e  

Alternativa (f) - n a n o b o d e  

Alternativa (g) - t e r a t o u r o  

Exercícios de Livros Relacionados

Um vetor A → aponta na direção + x . Mostre graficamente ao menos três escolhas para um vetor B → tal que B → + A → aponta na direção + y .
O prefixo mega significa (a) 10 - 9 , (b) 10 - 6 , (c) 10 - 3 , (d) 10 6 , (e) 10 9 .
O número 0,0005130 tem _____ algarismos significativos. (a) um, (b) três, (c) quatro, (d) sete, (e) oito.
Se x está em pés, t está em milissegundos, e v está em pés por segundo, quais são as unidades das constantes C 1 e C 2 em cada parte do problema 23 ?Itens do problema 23: (a) x = C 1 + C 2 t , (b) x =
Nas equações a seguir, a distância x está em metros, o tempo t está em segundos, e a velocidade v está em metros por segundo. Quais são as unidades do SI das constantes C 1 e C 2 ? (a) x = C 1 + C 2 t