Produto Vetorial
Produzido por Matheus dos Santos SoaresTeoria
O produto vetorial de dois vetores
Pra representar o produto vetorial, usamos a seguinte notação:
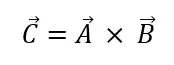
Se você ficou confuso, não se preocupa! Eu vou te explicar timtim por timtim! E pra começar com o pé direito, da uma conferida nesse vídeo supercompleto sobre produto vetorial 👇
Ou então, segue comigo no textinho! 👇
Como Calcular o Produto Vetorial?
E como a gente acha o vetor resultante de um produto vetorial?
Vamos aprender na prática, considera o seguinte produto vetorial
Para resolver esse problema, vamos usar um método em que a partir das componentes do produto vetorial, descobrimos as componentes do vetor resultante usando determinante!
O determinante é tranquilo, sempre vai ser um
A primeira linha ela vai servir como referência para saber qual número se refere a cada componente.
Na segunda linha, a gente coloca cada componente do primeiro vetor do produto vetorial, começando pela coordenada
Na terceira linha, a gente coloca cada componente do segundo vetor do produto vetorial, da mesma forma que fez com o primeiro vetor.
Montando o determinante, ficamos com:
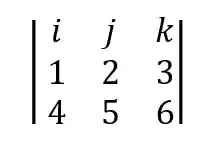
Não se lembra como faz
O vetor resultante é:
Regra da Mão Direita
A regra da mão direita vai salvar a nossa vida na hora da gente descobrir o sentido do vetor! 🤩
Ela é muito simples, da uma olhada nesse esquema aqui:
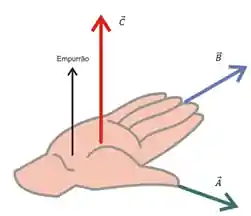
Vamos definir 3 partes da sua mão aqui:
- Dedão: O seu dedão vai ficar no sentido do primeiro vetor do produto vetorial
- Os seus 4 dedos (exceto seu dedão): Seus 4 dedos vão ficar no sentido do segundo vetor do produto vetorial
- Palma da mão: A palma da sua mão vai indicar o sentido do vetor resultante do produto vetorial
É importante que você perceba que faz diferença a ordem que você escolhe os vetores. Se a ordem for trocada, o sentido do vetor é diferente. Fazer com a mão esquerda não da certo também!
Módulo do Produto Vetorial
Na hora de calcular o módulo do produto vetorial, não tem mistério! É só usar essa fórmula aqui:
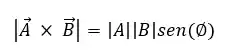
Essa fórmula vai ser muito útil pra gente, principalmente com relação ao ângulo entre os vetores.
Sacou tudo? Vamos praticar com exercícios?
Como Calcular o Produto Vetorial?
Regra da Mão Direita
Módulo do Produto Vetorial
Exercícios Resolvidos
Exercício Resolvido #1
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 34 –1.96.
Dois vetores e possuem módulo de e de . Seu produto vetorial é Qual é o ângulo entre e ?
Passo 1
Como foram dadas as componentes do , podemos calcular o módulo desse vetor, para depois usarmos a fórmula do produto vetorial.
Passo 2
Calculando o módulo do vetor
Substituindo as compenentes dadas temos:
Passo 3
Substituindo os valores no produto vetorial temos:
Isolando o , temos:
Epa! Pega a sua calculadora aí!
Resposta
Exercício Resolvido #2
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 34 –1.96
Para os vetores e indicados na figura abaixo:
- Ache o módulo e a direção do produto vetorial
- Ache o módulo e a direção do produto vetorial
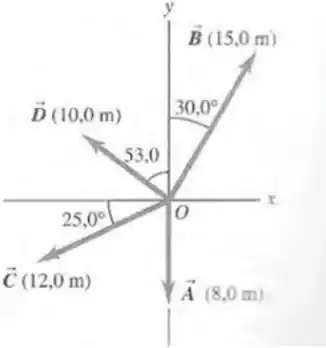
Dados:
Passo 1
Para calcularmos o módulo do produto vetorial vamos usar a seguinte fórmula:
É importante lembrar que o produto vetorial entre vetores não é comutativo, porém, pode ser considerado anti-comutativo?
Que???
Passo 2
Alternativa a)
Calculando o módulo de vetor:
Substituindo os valores na equação do módulo do vetor temos:
Passo 3
Alternativa b)
Calculando o módulo de vetor:
Substituindo os valores na equação do módulo do vetor temos:
Passo 4
Mas e a direção? Você não falou nada cara! Você deu a mesma resposta nas duas alternativas.
A direção dos vetores é a mesma. Os dois vetores passam pelo centro do eixo , perpendicular ao plano, pois os vetores precisam ser perpendiculares tanto à quanto à , na direção de .
Mas qual a diferença então?
A diferença é o sentido que os vetores possuem. Um vetor tem o sentido oposto ao outro.
Se você fizer a regra da mão direita , vai ver que o produto escalar de estará em e o será no sentido , que vai estar “furando” a tela do seu PC. :P
Resposta
Alternativa a),
Alternativa b)
Exercício Resolvido #3
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 33 –1.87- Modificado.
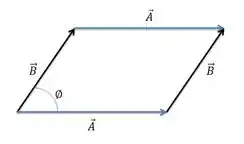
A figura abaixo mostra um paralelogramo cujos lados são os vetores e
- Mostre que o módulo do produto vetorial destes vetores é igual à área do paralelogramo . (Sugestão: )
- Qual é o ângulo entre o produto vetorial e o plano deste paralelogramo?
Passo 1
Sabemos que a fórmula do módulo de um produto vetorial é:
O que temos que fazer é provar que a área do paralelogramo tem essa mesma fórmula
Passo 2
Alternativa a)
O paralelogramo formado pelos vetores tem a seguinte forma:
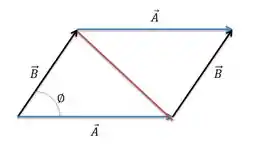
Como o problema deu uma dica, vamos usar, né?
Para calcular a área desse paralelogramo vamos dividir ele em dois triângulos, pois assim podemos usar a fórmula da área que ele deu.
Passo 3
Como podemos perceber, divimos á area do paralelogramo em dois triângulos iguais, ou seja, se acharmos a área do triângulo conseguimos achar a área do paraleogramo.
Para calcular a área do triângulo precisamos achar a altura relativa a base.
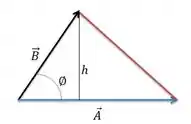
Considerando a altura relativa à base, temos que:
Passo 4
Como a fórmula da área de um triângulo é:
Substituindo os valores temos:
Escrevendo em função de :
Como já sabemos á relação da área do triângulo e do paralelogramo temos que:
Passo 5
Alternativa b)
Como os vetores formam um plano, que no caso é o plano do paralelogramo, e sabendo que o produto vetorial tem como resultado um vetor perpendicular à ambos, o vetor também é perpendicular ao plano formado pelos vetores:
Resposta
Exercício Resolvido #4
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 31 –1.52 e pp 28 – 1.25.
- Prove que dois vetores são anticomutativos para o produto vetorial, ou seja, prove que
- Se é necessariamente verdadeiro que Explique.
Passo 1
Alternativa a)
Se lembra como a gente calcula o produto vetorial por componentes? Então, vamos usar essa formula agora. Vamos supor dois vetores quaisquer, vamos trabalhar só com letras, ok? Sem números, é só comparativo.
Passo 2
Vamos calcular primeiro o produto vetorial
Calculando o determinante temos:
Passo 3
Agora vamos calcular o outro produto vetorial Se encontrarmos o mesmo valor conseguimos provar que o produto vetorial é anticomutativo.
Vamos calcular primeiro o produto vetorial
Calculando o determinante temos:
Reorganizando os sinais e os fatores temos:
Passo 4
Alternativa b)
Pra fazer essa questão vamos lembrar da fórmula do módulo do produto vetorial:
Passo 5
Alternativa a)
Pra fazer essa questão vamos analisar primeiro o lado direito da equação.
Vamos considerar que nem , e nem tem valor . Assim,
Assim, para o produto escalar ser , o ângulo entre os vetores teria que ser ou ou pois assim o . Isso significa que os dois vetores são paralelos!
Resumindo: .
Resposta
Exercício Resolvido #5
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 28 –1.23
Considere os dois produtos vetoriais repetidos e . Forneça um exemplo para mostrar que estes dois vetores normalmente não possuem nem módulo nem direções iguais. Você pode escolher os três vetores de modo que esses dois produtos vetoriais sejam iguais? Em caso afirmativo, forneça um exemplo.
Passo 1
Vamos usar 3 vetores escolhidos ao acaso para provar que normalmente os vetores não possuem nem módulo nem direções iguais
Escolhi vetores simples para não termos problemas nas contas. Números são um pouco chatinhos, ai acho melhor evitar =)
Passo 2
Alternativa a)
Vamos realizar uma operação de cada vez para não embolar a sua cabeça. A primeira que vamos fazer é
Calculando o produto vetorial
Assim temos como o vetor resultante
Passo 3
Calculando o produto vetorial entre
Depois de calcular o produto vetorial, a resposta da primeira equação é:
Passo 4
Agora vamos calcular a segunda equação, fechado?
Calculando o produto vetorial
Assim temos como o vetor resultante
Passo 5
Calculando o produto vetorial entre
Depois de calcular o produto vetorial, a resposta da segunda equação é:
Como os resultados foram diferentes, mostramos que normalmente os vetores não possuem módulos iguais, muito menos direções iguais.
Passo 6
Um modo fácil dos dois produtos serem iguais é todos os três vetores serem paralelos, pois assim, todos os produtos vetorais tem como resultado , pois vale .
Resposta
Exercício Resolvido #6
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 31 –1.56.
Por meio de desenhos simples dos produtos vetoriais aproximados, demonstre que pode ser interpretado como o produto do módulo de vezes o componente de perpendicular a ou o módulo de vezes a componente de perpendicular a
Passo 1
Sabemos que a fórmula do módulo de um produto vetorial é:
O que vamos fazer é demonstrar através da área de um paralelogramo que conseguimos encontrar essa fórmula.
Passo 2
O paralelogramo formado pelos vetores tem a seguinte forma:
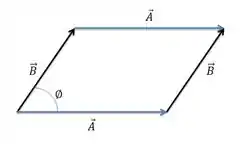
Para calcular a área desse paralelogramo vamos dividir ele em dois triângulos, pois assim podemos usar a fórmula da área que ele deu.
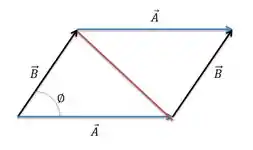
Passo 3
Como podemos perceber, divimos á area do paralelogramo em dois triângulos iguais, ou seja, se acharmos a área do triângulo conseguimos achar a área do paraleogramo.
Para calcular a área do triângulo precisamos achar a altura relativa a base.
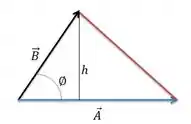
Considerando a altura relativa à base, ou seja, a componente vertical de em relação à temos que:
Passo 4
Como a fórmula da área de um triângulo é:
Substituindo os valores temos:
Escrevendo em função de :
Como já sabemos á relação da área do triângulo e do paralelogramo temos que:
Logo, como podemos ver, um produto vetorial pode ser escrito como:
onde é a componente de perpendicular a .
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 28 –1.19
Se são vetores diferentes de zero, é possível que e sejam ambos zero? Explique.
Passo 1
Bom, antes de analisar a afirmativa, vamos lembrar as fórmulas de cada um?
O produto escalar resulta em um número, dado por:
Já o produto vetorial resulta não em um número, mas em um outro vetor , cujo módulo é dado por:
Ou simplesmente, podemos escrever os módulos apenas com as letras sem a setinha:
Passo 2
Como os módulos dos vetores são diferentes de zeros (tá no enunciado, checa lá), o que fica em jogo aqui é o . Como os dois não podem ser zero ao mesmo tempo, é impossível as duas expressões serem ambas zero.
:D
Resposta
Exercício Resolvido #8
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp. 28 –1.22.
Quais das seguintes operações são legítimas:
Forneça a razão da resposta em cada caso.
Passo 1
Alternativa a)
Legitima
A operação é uma operação normal de subtração de vetores e com o vetor resultando é feito um produto escalar com o vetor .
Passo 2
Alternativa b)
Legitima
A operação é uma operação normal de subtração de vetores e com o vetor resultando é feito um produto vetorial com o vetor .
Passo 3
Alternativa c)
Legitima
A operação é um produto vetorial entre dois vetores, que gera um vetor resultante, que faz um produto escalar com o vetor
Passo 4
Alternativa d)
Legitima
A operação é um produto vetorial entre dois vetores, que gera um vetor resultante, que faz um produto vetorial com o vetor
Passo 5
Alternativa e)
Ilegitima
A operação é um produto escalar entre dois vetores, que gera um número resultante, que faz um produto vetorial com o vetor , o que é errado, pois um produto vetorial precisa ser necessariamente entre dois vetores.
Resposta
- Legitima
- Legitima
- Legitima
- Legitima
- Ilegítima
Exercício Resolvido #9
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp. 28 –1.24.
Demonstre que, não importa o que sejam, e , .
(Sugestão: não procure uma prova matemática elaborada. Em vez disso, examine a definição da direção do cross product).
Passo 1
Bom, já que a questão deu dica, vamos usar, né? Hahahhahaa
O produto vetorial vai gerar um vetor(ahhh, vá?) que é perpendicular ao mesmo tempo à ou seja, o ângulo entre o vetor resultante é os vetores do produto vetorial é
Passo 2
Se lembra como varia o produto escalar de acordo com o ângulo entre os vetores? Então, só com isso a gente já mata a questão: sempre que o ângulo entre dois vetores é o produto escalar entre eles vale .
Resposta
Ei, a resposta está no passo a passo :)