Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.10 - Ex. 56b
Por meio de desenhos simples dos produtos vetoriais apropriados, demonstre que
b) pode ser interpretado como o produto do módulo de vezes o componente de perpendicular a , ou o módulo de vezes o componente de vezes o componente de perpendicular a .
Passo 1
Fala aí, pessoal! 😉
Nesse problema temos que mostrar que pode ser interpretado como o produto do módulo de vezes o componente de perpendicular a , ou o módulo de vezes o componente de vezes o componente de perpendicular a .
Tem ideia de como fazemos isso? 😊
Sabemos que a fórmula do módulo de um produto vetorial é:
O que vamos fazer é demonstrar através da área de um paralelogramos que conseguimos encontrar essa fórmula.
Veja só! 👀
Passo 2
O paralelogramo formado pelos vetores tem a seguinte forma:
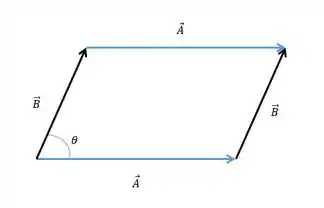
Para calcular a área desse paralelogramo vamos dividir ele em dois triângulos, pois assim podemos usar a fórmula da área.
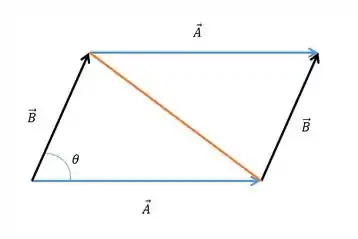
Tranquilo até aqui? 😁
Passo 3
Como podemos perceber, dividimos a área do paralelogramo em dois triângulos iguais, ou seja, se acharmos a área do triângulo conseguimos encontrar a área do paralelogramo.
Para calcular a área do triângulo precisamos achar a altura relativa a base.
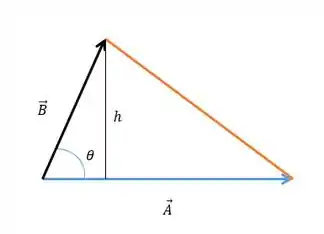
Considerando a altura relativa à base, ou seja, a componente vertical de em relação à temos que :
bacana, não é? 😉
Passo 4
Como a fórmula da área de um triângulo é:
Substituindo valores, temos:
Escrevendo em função de
Como já sabemos a relação da área do triângulo e do paralelogramo, temos que:
Logo, como podemos ver, um produto vetoria pode ser escrito como:
Onde é a componente de perpendicular a .
E aí! entendeu tudo? Responde Aí! 😁
