Força de Arraste e Velocidade Terminal
Produzido por Ludovic BeghinTeoria
Fala aí! Hoje, vamos trocar uma ideia sobre força de arraste e velocidade terminal.
Só pra deixar claro, o foco dessa página é te ensinar como resolver exercícios de leis de Newton envolvendo esses carinhas aí. Mas não se preocupa! Se você clicou aqui querendo aprender sobre força de arrasto da camada limite lá da matéria de Fenômenos de Transporte e Mecânica dos Fluidos, se liga no primeiro link que vou deixar aqui embaixo com esse conteúdo prontinho pra você 👇😉
⭐ Veja também ⭐
- Força de Arrasto, Arrasto de Atrito e Arrasto de Pressão.
- Introdução à Camada Limite.
- Leis de Newton - Resumo.
- Força de Atrito.
O que é a força de arraste?
A força de arraste é aquela que surge da resistência de fluidos (líquidos e gases) oposta a corpos que os atravessam.
Já tentou correr rapidão dentro de uma piscina? Ou sentiu um pouquinho de dificuldade pra se manter firme no chão em um dia de ventos muito fortes? Tudo isso são exemplos de fluidos exercendo um arraste no seu corpinho ☺️
Na maioria dos exercícios que vemos desde a escola, somos direcionados a desprezar o atrito e outras forças dissipativas, mesmo sabendo que esses caras tem um grande impacto em situações reais!
Agora, você já está pronto para passar para o próximo nível e para de desprezar esses coitados!
Como calcular a força de arraste?
A força de arraste é proporcional ao coeficiente de arraste (C), à massa específica do fluido (
Tudo isso faz muito sentido, não é mesmo?
Vamos pensar na situação da piscina novamente, se você tenta mover sua mão de um lado pro outro, como se fosse dar um tapa em alguém, embaixo d’água:
- a força que precisa fazer é maior do que se tentasse o mesmo movimento fora d’água, porque a água é mais densa (maior massa específica) do que o ar.
- se sua mão estiver completamente aberta e com a palma virada na direção do movimento, é preciso menos força do que se sua mão estiver fechada ou com a palma posicionada paralelamente ao movimento (no primeiro caso, sua mão tem maior área de seção transversal).
- por fim, quanto mais rápido você tenta mexer a mão, maior a força necessária para vencer a resistência da água.
Assim, a gente evidencia como a força de arraste é proporcional a todos esses fatores! 😄
Bora tentar resolver um exercício aplicando o que acabamos de aprender? Se liga nesse aqui resolvido bem passo a passo 👇
Nosso mascote Dexter, que possui uma massa de 20 kg, se joga de uma altura H = 10 m com uma velocidade inicial nula. Se considerarmos que Dexter possui uma área transversal A = 150 cm² e que a densidade do ar é
Se chamarmos de
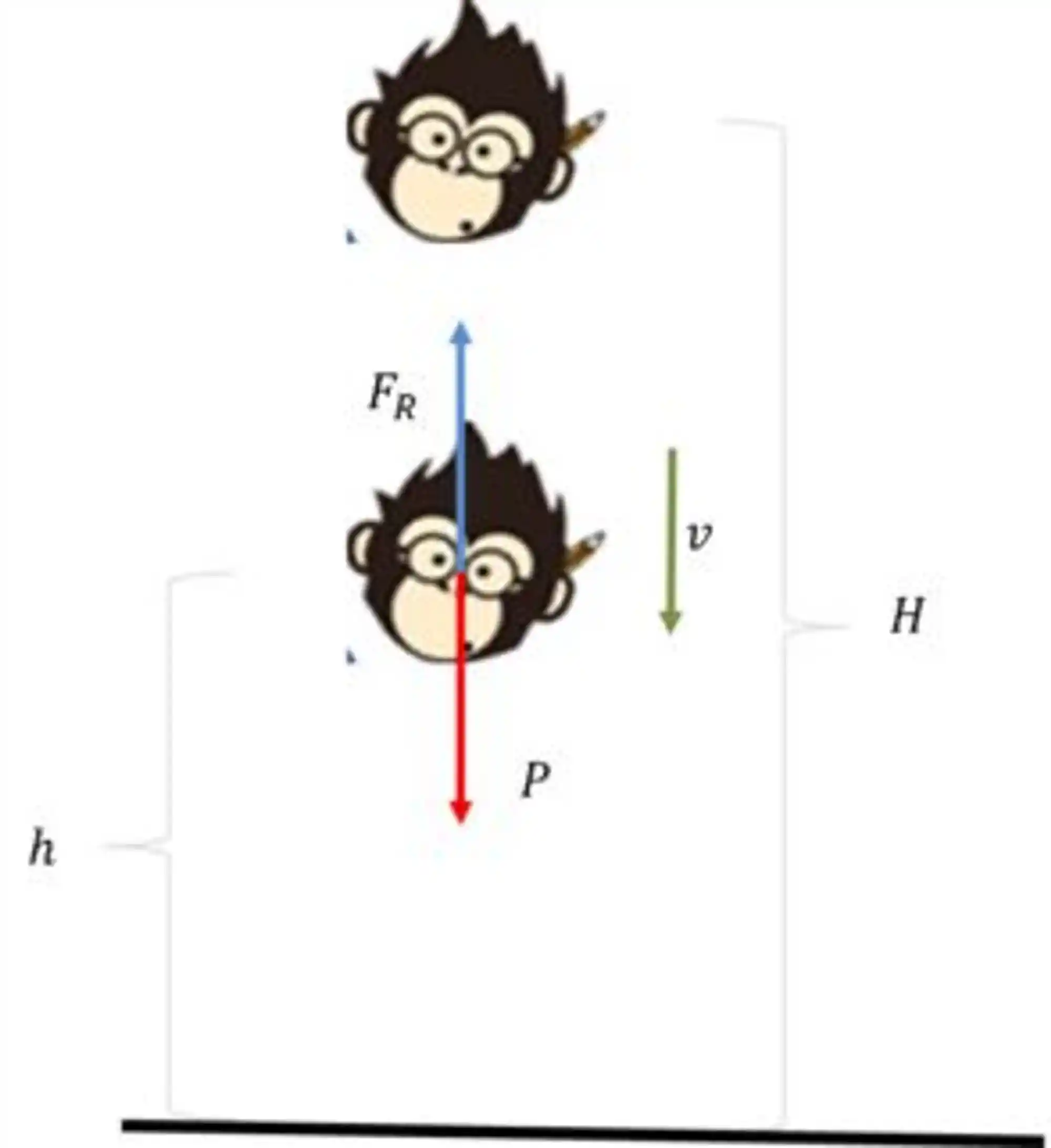
Aí, a expressão da segunda lei de Newton fica assim:
E, se substituirmos as expressões conhecidas para cada força:
O enunciado nos pede a velocidade terminal, bora entender um pouquinho melhor isso aí antes de continuarmos o exercício?
O que é velocidade terminal?
A velocidade terminal é a velocidade de um objeto em queda livre. Ou, a velocidade máxima de um corpo em movimento em um fluido, obtida quando a força resultante sobre ele se torna nula (em palavras mais refinadas).
No exemplo anterior, podemos traçar um gráfico que mostre como as duas forças que agem sobre o Dexter variam com o tempo:
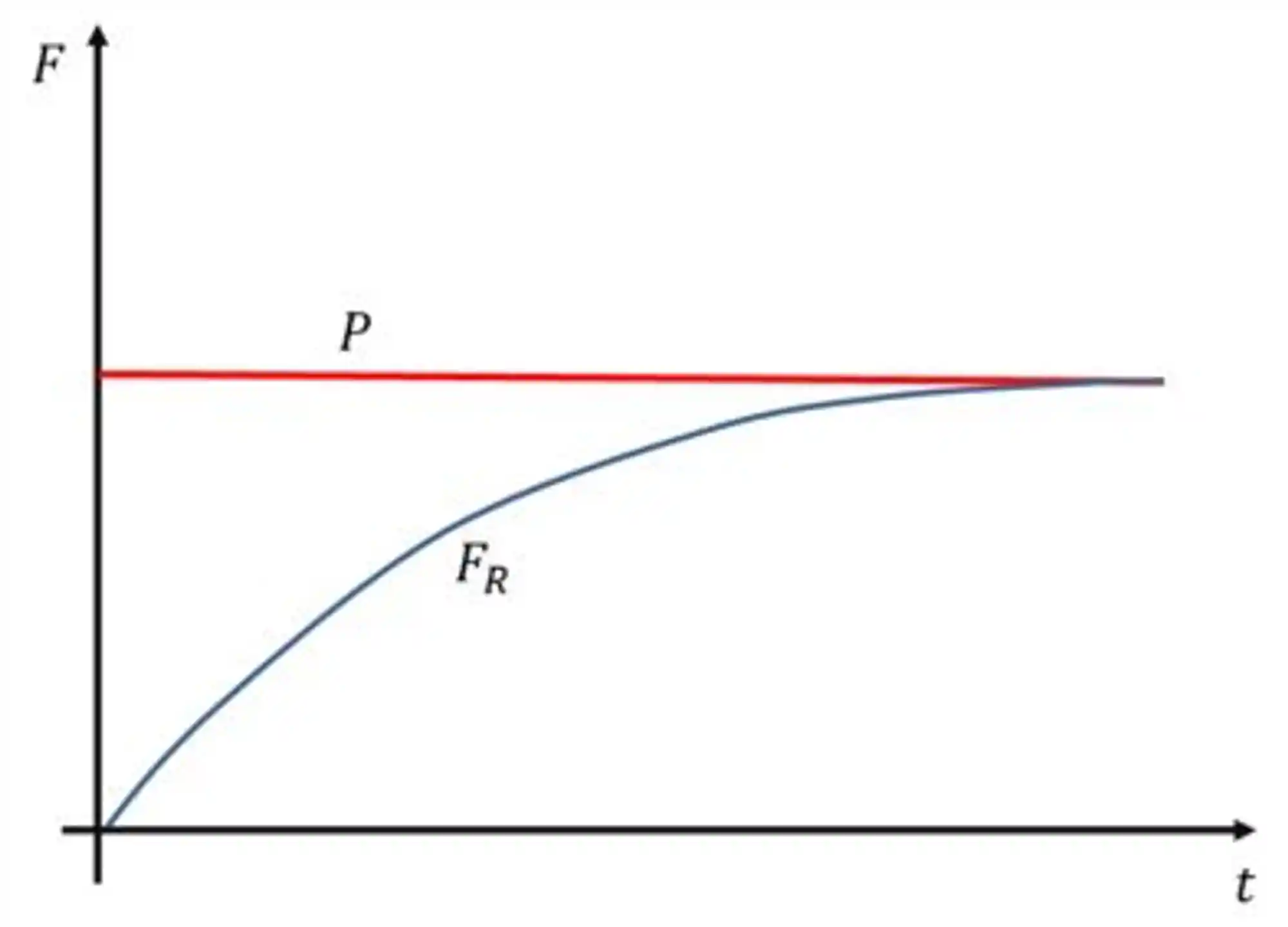
Repare que a força peso é constante, afinal, tanto a massa do corpo quanto a gravidade são constantes em todos os cenários que vamos considerar. Enquanto a força de arraste é proporcional ao quadrado da velocidade.
Nota-se, que a velocidade cresce até atingir um limite, no qual a aceleração é nula. Neste ponto, temos:
Assim, podemos obter a expressão para a velocidade terminal:
Agora sim, podemos finalizar nosso exercício anterior. Bora substituir os valores:
Em uma queda de 10 m, partindo do repouso, é bem improvável que o Dexter atinja uma velocidade dessas!
Vamos subir o nível ainda mais um pouquinho com os nossos exercícios selecionados a seguir!
O que é velocidade terminal?
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, David, Fundamentos de física, volume 1 - mecânica, 8 ed. Rio de Janeiro : TLC, 2008, p. 145 ex. 36
A velocidade terminal de um pára-quedista é de na posição de águia e na posição de mergulho de cabeça. Supondo que o coeficiente de arrasto do pára-quedista não mude de uma posição para outra, determine a razão entre a área da seção reta efetiva na posição de menor velocidade e a área na posição de maior velocidade.
Passo 1
Sabemos que a expressão da velocidade terminal é dada por:
Se isolarmos a área de seção reta:
Passo 2
Portanto, para a relação entre as áreas, temos:
Substituindo os valores:
Resposta
Exercício Resolvido #2
Halliday, David, Fundamentos de física, volume 1 - mecânica, 8 ed. Rio de Janeiro : TLC, 2008, p. 145 ex. 27
Calcule a razão entre a força de arrasto experimentada por um avião a jato voando a a uma altitude de e a força de arrasto experimentada por um avião com metade da velocidade e a metade da altitude. A densidade do ar é de a e a . Suponha que os aviões possuem a mesma área de seção reta efetiva e o mesmo coeficiente de arrasto .
Passo 1
Sabemos que a expressão da força de arrasto é:
Se fizermos a relação:
E substituirmos os valores:
Resposta
Exercício Resolvido #3
Halliday, David, Fundamentos de física, volume 1 - mecânica, 8 ed. Rio de Janeiro : TLC, 2008, p. 148 ex. 73
Qual é a velocidade terminal de uma bola esférica de que possui um raio de e um coeficiente de arrasto de ? A massa específica do ar no loca onde a bola está caindo é .
Passo 1
Aqui é pura aplicação da fórmula da velocidade terminal:
Substituindo os valores:
Resposta
Exercício Resolvido #4
Halliday, David, Fundamentos de física, volume 1 - mecânica, 8 ed. Rio de Janeiro : TLC, 2008, p. 147 ex.76
Calcule o módulo da força de arrasto a que está sujeito um míssil de de diâmetro voando a em baixa altitude. Suponha que a massa específica do ar é de e o coeficiente de arrasto é de .
Passo 1
Vamos usar aqui a fórmula da força de arrasto:
Substituindo os valores: