Você e seus amigos empurram um porco engordurado de para cima sobre um escorregador de alumínio na feira local, começando da extremidade inferior do escorregador. O coeficiente de atrito cinético entre o porco e o escorregador é . (a) Todos vocês estão empurrando juntos (paralelamente à inclinação), e conseguem acelerar o porco a partir do repouso à taxa constante de por uma distância e , e então soltam o porco. O porco continua subindo o escorregador até atingir uma altura vertical máxima acima do ponto onde foi solto, a de altura. Qual é o ângulo de inclinação do escorregador? (b) Na altura máxima o porco inverte o seu sentido e começa a escorregar para baixo, quão rápido ele está se movendo quando chega na extremidade inferior do escorregador?
Passo 1
a) Olá, querido! Tá bem? Então, temos um porquinho sendo empurrado por uma rampa. Ele sai do repouso e atinge uma velocidade depois de ser empurrado por com uma aceleração .
Depois de atingir , ele não é mais empurrado mas continua a subir, até que atinge a altura máxima de em relação ao ponto onde tinha .
Um esqueminha do que aconteceu é:
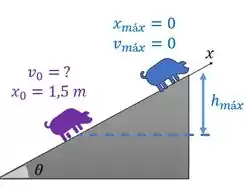
Repara que o eixo está na direção da trajetória.
E aí o que ele pede é o valor de . Bora descobrir!
Passo 2
Vamos começar pensando no trecho que o porco sobe após ser empurrado por .
Ao ser solto, ele tem uma velocidade inicial , e vai “frear” depois de percorrer uma distância até parar no topo da sua trajetória. Então a gente tem um movimento acelerado. Como não temos o tempo, podemos usar a equação de Torriceli:
A velocidade no ponto máximo é nula :
Onde é a aceleração do porco “livre” (depois de ser solto).
Ok, e como podemos achar a velocidade ? Essa é a velocidade que o porco ganha depois de ser acelerado a por partindo do repouso. Vamos usar Torriceli de novo, mas agora para esse trecho:
Nesse caso, porque o porco sai do repouso, é a velocidade no final do percurso, e . Substituindo:
Substituindo isso na equação :
Passo 3
O enunciado também dá a altura máxima que ele sobe enquanto anda uma distância pelo plano, como estamos em um plano inclinado, a relação entre e pode ser achado por trigonometria:
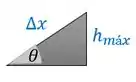
Daí tiramos:
Então a equação fica:
E fica faltando encontrar uma expressão para a aceleração do porco livre.
Passo 4
Quem causa a desaceleração do porco é o atrito entre ele e a rampa. Então teremos uma força de atrito se opondo ao movimento dele, que está subindo a rampa. Então a força aponta para o sentido oposto:
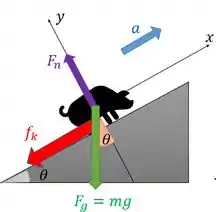
A partir desse diagrama, a gente pode usar a segunda lei de Newton e achar . Vamos assumir o sistema de coordenadas como está indicado na figura acima. A única força que não está nos eixos é a força peso, então devemos decompô-la nos eixos x e y, dessa forma:
De acordo com a 2° Lei de Newton no eixo x, temos:
As duas forças aparecem negativas no somatório porque ambas apontam para o sentido negativo de . Lembrando que :
Só que essa força de atrito é a força de atrito cinético, que vale
Onde é o coeficiente de atrito cinético dado no enunciado. Substituindo
Falta a gente achar .
Passo 5
A 2° Lei de Newton em y, como a soma das forças em y é igual a zero, já que , pois o porco não se move em , fica:
Substituindo isso em :
Isolando :
Substituindo na equação do passo 3
Isolando (já que a gente quer ):
Passo 6
(b) Agora queremos saber a rapidez do porco quando ele chega no final da rampa, depois de descer lá da altura máxima. Ou seja, a rapidez quando ele chega no ponto onde começou a ser empurrado.
Nessa descida, a distância percorrida vai ser (que é a distância que ele foi empurrado) mais (a distância que ele subiu), só ambas serão deslocamentos negativos porque estão no sentido contrário de :
A velocidade inicial desse novo percurso é zero.
E só precisamos fazer uma pequena mudança na nossa aceleração de porco livre para achar , já que o sentido da força de atrito para o novo percurso vai ser igual porém apenas invertida. Então a gente vai pegar nossa expressão de e apenas mudar o sinal do termo que tem o coeficiente de atrito:
Agora é só substituir na mesma equação de Torriceli para saber a velocidade do porco no final do percurso:
Substituindo os dados:
Resposta
(a) .
(b) .