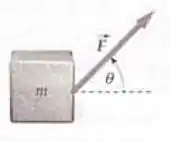
Considere o bloco da figura abaixo. Mostre que, em geral, os seguintes resultados valem para um bloco de massa que está sobre uma superfície horizontal de coeficiente de atrito estático . (a) Se você deseja aplicar a menor força possível para mover o bloco, você deve aplicá-la puxando para cima a um ângulo . (b) A força mínima necessária para começar a mover o bloco é . (c) Uma vez iniciado o movimento do bloco, se você deseja aplicar a menor força possível para mantê-lo em movimento, você deve manter o ângulo com o qual você está puxando, deve aumentá-lo ou deve diminuí-lo?

Agora em x:

Agora gente joga a (1) na (2):

A gente quer a menor força possível, certo? Então a gente precisa do maior denominador. Vamos olhar para a função:

Se a gente quer maximizar a função, vamos derivar e igualar a zero:

Letra (b)

Vamos aplicar o resultado da letra (a) lá na equação (3). Mas primeiro vamos ver quanto vale o seno e o cosseno de :

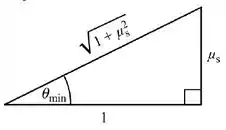
Da figura, a gente vê que:

e

Agora sim, jogando na (3):

Aí a gente chegou no resultado:

Letra (c)

A gente sabe que quando o atrito passa do estático para o cinético o coeficiente de atrito diminui. Só que olha só: se a gente repetir o mesmo cálculo da letra (a), a gente acha que o ângulo para a menor força é . Só que , então a gente deve diminuir o ângulo.