Força Elástica
Produzido por Ludovic BeghinTeoria
Força elástica
-Hãam?! 😖
Imagina a seguinte situação:
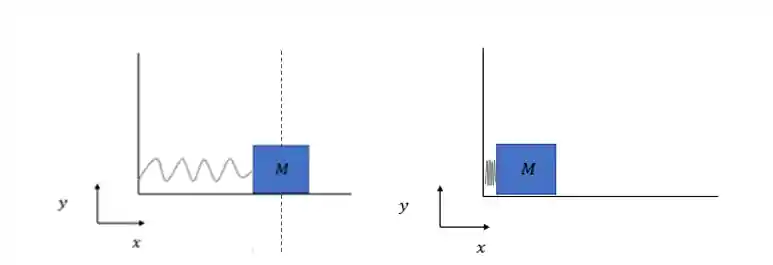
No primeiro momento temos um bloquinho preso por uma mola e depois o bloquinho é empurrado, comprimindo a mola até a parede.
Porém se você soltar o bloquinho, ele vai voltar a posição inicial não vai? Por que?
Por causa da força elástica! Ela é a responsável por esse fenômeno, fazendo a mola voltar pra posição inicial. Se você puxasse a mola a força elástica também apareceria lá na tentativa de voltar para a posição inicial, porém em outro sentido.
Como Calcular a Força Elástica?
Pra a gente entender como calcular a força elástica, vamos usar o exemplo da imagem que vimos lá em cima:
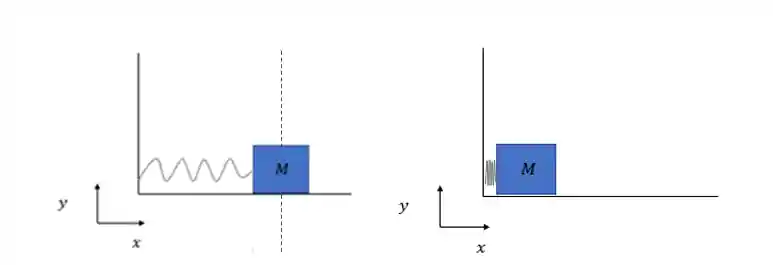
Qual é o módulo da força elástica da mola, se a mola se deformou
Fórmula da Força Elástica - Lei de Hooke
A lei de Hooke diz que quando uma mola é deformada por uma força externa, uma força elástica passa a ser exercida em oposição à força externa.
Para calcular a força elástica usamos a seguinte fórmula:
Onde:
é a força elástica medida em Newtons; é a constante elástica ; é a deformação da mola .
Calculando a Força Elástica
O nosso problema pediu pra calcularmos o módulo da força elástica, então teremos:
O sinal negativo vai embora!
Sabemos que, a mola se deformou
Aweee!!
Vídeo Aula - Força Elástica
Ficou com alguma dúvida?! Então confere essa vídeo aula super completa que a gente preparou pra você! 👇
Agora vamos praticar com exercícios?!
Como Calcular a Força Elástica?
Vídeo Aula - Força Elástica
Exercícios Resolvidos
Exercício Resolvido #1
Mack-1996
Para a verificação experimental das leis da Dinâmica, foi montado o sistema a seguir:
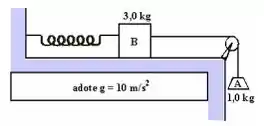
Nele, o atrito é desprezado, o fio e a aceleração são ideais. Os corpos A e B encontram-se em equilíbrio quando a mola “ultraleve” M está distendida de . A constante elástica dessa mola é:
Passo 1
Foi dito que o sistema está em equilíbrio, portanto, a resultante das forças que agem nos dois corpos são necessariamente nulas, segundo a primeira lei de Newton.
Começemos então fazendo o diagrama de corpo livre do peso pendurado A:
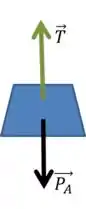
Como a resultante tem que ser zero:
Sabemos o valor de , portanto:
Passo 2
Já para o bloco B, temos:
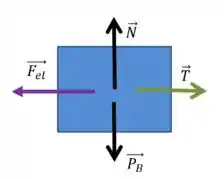
Apesar de existir, o equilíbrio do bloco na direção do eixo não é interessante para nós, já que não nos trará nenhum resultado relevante. Portanto, vamos analisar somente o equilíbrio na direção do eixo :
Como sabemos, a tensão é a mesma para um mesmo fio, portanto:
Aprendemos pela lei de Hook que:
O valor de foi dado, ele é a distensão da mola e vale , portanto, juntando as duas equações, temos:
E chegamos então à resposta:
Resposta
Alternativa B
Exercício Resolvido #2
Mack-1996
O esquema apresenta um elevador que se movimenta sem atrito. Preso a seu teto, encontra-se um dinamômetro que sustenta em seu extremo inferior um bloco de ferro. O bloco pesa mas o dinamômetro marca . Considerando , podemos afirmar que o elevador pode estar:
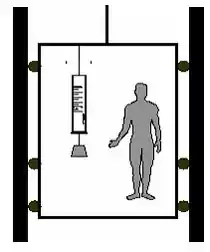
- Em repouso
- Descendo com velocidade constante
- Descendo em queda livre
- Descendo com movimento acelerado de aceleração de
- Subindo com movimento acelerado de aceleração de
Passo 1
Apesar de não ser dito no enunciado, temos que considerar que neste problema o bloco de ferro está em repouso em relação ao homem que se encontra dentro do elevador.
Como os outros problemas, precisamos relacionar força e aceleração. Usaremos então a segunda lei de Newton!
Mas, antes de partir pra resolução, temos que entender como funciona o dinamômetro. O que significa o dinamômetro estar marcando ?
O dinamômetro nada mais é do que uma mola com um gancho, onde a constante elástica dessa mola é conhecida. Assim, usando a Lei de Hook, podemos sempre relacionar a deformação da mola com a força aplicada no gancho em sua extremidade.
Podemos agora fazer o diagrama de corpo livre do bloco de ferro, temos então:

O módulo da é, segundo a terceira lei de Newton, a reação que o gancho do dinamômetro aplica no bloco de ferro, portanto, aplicando a segunda lei de Newton, temos, supondo que existe uma aceleração e que ela está para baixo:
Substituindo os valores conhecidos:
E com isso concluímos que:
Como deu negativo, nossa suposição estava errada e, portanto, o bloco está subindo com aceleração
Resposta
Alternativa E
Exercício Resolvido #3
Elaboração Própria
Dois blocos e , de massa e respectivamente, estão apoiados em um plano inclinado sem atrito. Eles estão presos entre si por um fio, enquanto o bloco é mantido em repouso por estar preso a parede por uma mola, tendo sua constante elástica igual a . Determine O valor da força de tração no fio e o valor da deformação da mola.
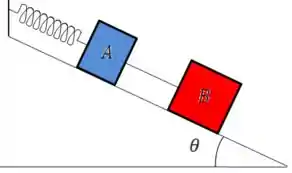
Passo 1
Os dados do problema são
Em problemas literais é sempre bom escrever os dados separados para mais tarde conferir se as respostas estão de acordo com esses dados.
Antes de fazer o DCL de cada bloco, vamos fazer algo que facilita nossas contas, o DCL do sistema. Considerando e uma coisa só.
Vamos responder as perguntas do passo a passo para colocar as forças
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
Sim, ele tem massa.
Sim, o sistema está apoiado no chão.
Não, não existe fio atuando.
Sim, temos uma mola.
O DCL do sistema fica
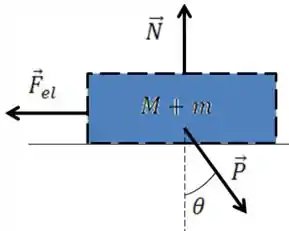
Assim, é mais fácil considerarmos a horizontal e vertical em relação à superfície inclinada, isso facilita nossas contas porque ele não tem movimento vertical em relação a essa superfície.
Passo 2
Como o sistema está em repouso, temos equilíbro em ambos os eixos. Estamos procurando a deformação da mola, então vamos usar o por ele conter a força elástica.
Devemos encontrar usando a “regra do COlado, SEparado”.
Passo 3
Para encontrar a força de tração, precisamos apenas fazer o DCL de um dos blocos, iremos fazer do bloco , respondendo as perguntas do passo a passo
Vamos responder as perguntas do passo a passo para colocar as forças
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
Sim, ele tem massa.
Sim, o sistema está apoiado no chão.
Sim, existe um fio.
Não, não existe uma mola atuando.
O seu DCL fica
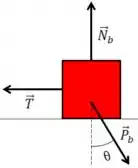
O ângulo fica na força peso com a vertical
O bloco está em equilíbrio, então faremos o equilíbrio no , porque é nele onde está a força de tração.
Devemos encontrar usando a “regra do COlado, SEparado”.
Resposta
Exercício Resolvido #4
Elaboração própria
Temos dois blocos e dispostos em uma cunha presos entre si por um fio, enquanto o bloco está preso ao chão por uma mola de constante elástica , como mostrado na figura abaixo. Sabendo que suas massas são e , respectivamente e que o atrito é desprezível. Determine a deformação da mola e a força de tração no fio, sabendo que os blocos estão em repouso. Considere ainda os ângulos mostrados na figura como dados, e o módulo da aceleração da gravidade como .
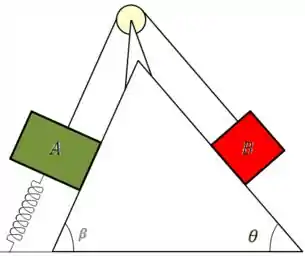
Passo 1
Normalmente começamos um problema com vários blocos, fazemos o DCL do sistema. Neste caso, como temos os blocos em repouso, ou seja, em equilíbrio fazer o sistema pode ser algo mais complicado, então iremos montar as equações para cada bloco.
Os dados do problema são
Em problemas literais é sempre bom escrever os dados separados para mais tarde conferir se as respostas estão de acordo com esses dados.
Para o bloco
Vamos responder as perguntas do passo a passo para colocar as forças
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
Sim, ele tem massa.
Sim, o bloco está apoiado na superfície inclinada.
Sim, existe um fio.
Não, não existe mola atuando.
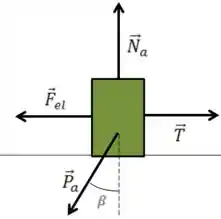
Quando temos um exercício de plano inclinado, é mais fácil considerarmos a horizontal e vertical em relação à superfície inclinada, isso facilita nossas contas porque ele não tem movimento vertical em relação a essa superfície. O DCL ficaria
O ângulo fica na força peso com a vertical
Passo 2
Como o bloco está em equilíbrio, não faz diferença qual eixo vamos escolher para começar o problema, porem como a força que nos interessa é a tração, não precisamos fazer as contas ao longo do . No , que está em equilíbrio,
Devemos encontrar usando a “regra do COlado, SEparado”.
Passo 3
Para o bloco
Vamos responder as perguntas do passo a passo para colocar as forças
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
Sim, ele tem massa.
Sim, o bloco está apoiado na superfície inclinada.
Sim, existe um fio.
Sim, existe uma mola.
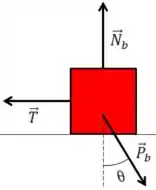
Quando temos um exercício de plano inclinado, é mais fácil considerarmos a horizontal e vertical em relação à superfície inclinada, isso facilita nossas contas porque ele não tem movimento vertical em relação a essa superfície. O DCL ficaria
O ângulo fica na força peso com a vertical
Nesse DCL temos um pequeno problema, como não sabemos qual bloco estaria descendo caso o bloco não estivesse preso no chão pela mola, vamos considerar o sentido da força elástica para esquerda, isso quer dizer q o bloco estaria descendo. Vamos ver como resolver esse problema de sentido já já.
Passo 4
No , como está em equilíbrio,
Devemos encontrar usando a “regra do COlado, SEparado”.
Como queremos que seja positivo basta colocarmos em módulo
Dessa forma garantimos que é positivo.