Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 5.Problemas - Ex. 6
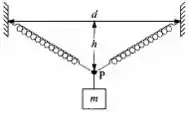
O sistema da figura está em equilíbrio. A distância d é de 1m e o comprimento relaxado de cada uma das duas molas iguais é de 0,5 m. A massa m de 1 Kg faz descer o ponto P de uma distância h=15 cm. A massa das molas é desprezível. Calcule a constante k das molas.
Passo 1
Galera, a primeira coisa a se fazer é calcular o comprimento das molas para saber sua distensão, ok? Usando simplesmente Pitágoras fica assim
Como o comprimento de repouso da mola é de
Passo 2
Pronto, nossa equação de hooke nos diz que só precisamos achar a força elástica agora para descobrir a constante k, tranquilo? Vamos olhar para o diagrama de forças na caixa.
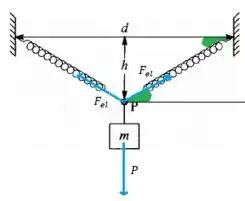
( nosso ângulo verde)
As forças horizontais se equilibram então vamos olhar para as componentes verticais no sistema. Sabemos que
Além disso,
Agora é só olhar pra nossa fórmula isolando a força elétrica
Passo 3
Agora é só pôr na lei de hooke que é sucesso, vem comigo!