Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 2.4 - Ex. 30
Para um carro para em um semáforo. Quando a luz fica verde, o carro começa a acelerar com uma taxa constante, elevando sua velocidade para , depois de a luz ficar verde. Ele se move com essa nova velocidade por uma distância de . A seguir, o motorista avista uma luz vermelha no cruzamento seguinte e começa a diminuir a velocidade com uma taxa constante. O carro pára no sinal vermelho a da posição para .
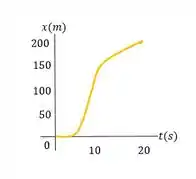
a) Para o movimento do carro, desenhe gráficos acurados de , e .
b) Faça um diagrama do movimento (como o da Figura 2.13b ou o da Figura 2.14 b) mostrando a posição, a velocidade e a aceleração do carro.
Passo 1
Opa, bora resolver esse problema. Temos um carro que sai do repouso quando a luz do semáforo fica verde e segue em uma aceleração constante.
Inicialmente temos que:
Nos próximos ele mantêm a velocidade de . Logo depois a velocidade começa a diminuir a uma taxa constante. Ou seja, vamos ter uma aceleração negativa constante! Depois disso temos que:
Vamos tomar a direção positiva, . E sabemos que a posição inicial do carro, no primeiro semáforo é de .
Passo 2
- Agora vamos calcular a posição do carro num intervalo de tempo de a , ou seja: .
Então, vamos calcular sua aceleração:
O carro se move de até . A velocidade, , aumenta linearmente de zero até e aceleração constante, .
Como temos velocidade constante por uma distância de e o corre se move da posição até e velocidade constante, . E aceleração, .
O intervalo de tempo, começa em e termina em:
Passo 3
Agora temos que o carro diminui sua velocidade até parar no próximo semáforo, então temos que o carro se move de para , de uma velocidade até zero.
Precisamos calcular quanto tempo o carro leva até parar:
Isolando , temos que:
Assim,
Em seguida, vamos calcular a desaceleração até que o carro pare:
Essa parte do movimento do carro acontece no intervalo de tempo de a e aceleração constante, .
Passo 4
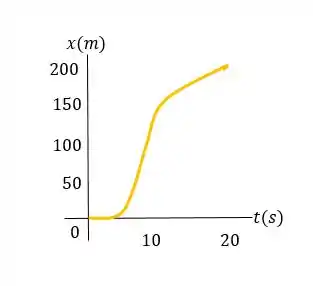
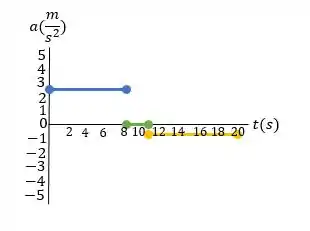
Quando e estão na mesma direção, a velocidade aumenta a
Quando e estão em direções opostas, a velocidade diminui a
Quando a aceleração é igual a zero, a velocidade é constante a
Resposta
