Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 2.Problemas Adicionais - Ex. 93

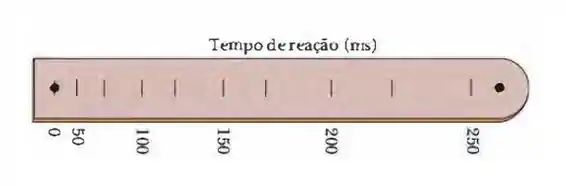
A Fig. 2-42 mostra um dispositivo simples que pode ser usado para medir o seu tempo de reação: uma tira de papelão marcada com uma escala e dois pontos. Um amigo segura a tira na vertical, com o polegar e o indicador no ponto da direita da Fig. 2-42. Você posiciona o polegar e o indicador no outro ponto ( o ponto da esquerda da Fig. 2 - 42), sem tocar a tira. Seu amigo solta a tira e você tenta segurá-la assim que percebe que começou a cair. A marca na posição em que você segura a tira corresponde ao seu tempo de reação.

(a) A que distância do ponto inferior você deve colocar a marca de 50,0   m s ? Por que valor você deve multiplicar essa distância para determinar a marca de (b) 100   m s , (c) 150   m s , (d) 200   m s , e (e) 250   m s ?

(Por exemplo: a marca de 100   m s deve estar no dobro da distância correspondente à marca de 50   m s ? Nesse caso, a resposta seria 2 . Você é capaz de identificar algum padrão nas respostas?)

Passo 1

Para começar, precisamos ter em mente que, ao soltar a tira, ela começa a pecorrer toda extensão em MRUV. A velocidade inicial é nula, pois o mesmo parte do repouso no ponto zero. Vamos considerar que o movimento ocorre no eixo y e que o y + seja vertical para baixo.

Lembrando que precisamos ter uma unificação das unidades, então quando usarmos os tempos dados no problema multiplicaremos por um fator de 10 - 3 para transformar de m s para s .

Passo 2

Observando o os dados dado pela questão, podemos utilizar a equação da posição do MRUV para determinar a que distância do ponto inferior você deve colocar a marca de 50,0   m s :

∆ y = v o t + 1 2 × a × t 2

∆ y 1 = 0 × 50 + 1 2 × 9,8 × ( 50 × 10 - 3 ) 2

∆ y 1 = 0 + 12250

∆ y 1 = 0,012   m

Passo 3

Fazendo de modo análogo para determinar no tempo de 100   m s :

∆ y = v o t + 1 2 × a × t 2

∆ y 2 = 0 × 100 + 1 2 × 9,8 × ( 100 × 10 - 3 ) 2

∆ y 2 = 0 + 0,049   m

∆ y 2 = 0,049   m

Passo 4

No tempo de 150   m s :

∆ y = v o t + 1 2 × a × t 2

∆ y 3 = 0 × 100 + 1 2 × 9,8 × ( 150 × 10 - 3 ) 2

∆ y 3 = 0 + 0,110

∆ y 3 = 0,110   m

Passo 5

No tempo de 200   m s :

∆ y = v o t + 1 2 × a × t 2

∆ y 4 = 0 × 100 + 1 2 × 9,8 × ( 200 × 10 - 3 ) 2

∆ y 4 = 0 + 0,196

∆ y 4 = 0,196   m

Passo 6

No tempo de 250   m s :

∆ y = v o t + 1 2 × a × t 2

∆ y 5 = 0 × 100 + 1 2 × 9,8 × ( 250 × 10 - 3 ) 2

∆ y 5 = 0 + 0,306

∆ y 5 = 0,306   m

Passo 7

Agora, vamos analisar se há algum tipo de padrão. Para começar, vamos testar para ver se os valores são múltiplos uns dos outros:

∆ y 2 ∆ y 1 = 0,0 49 0,012 = 4,0

∆ y 3 ∆ y 1 = 0,110 0,012 = 9,2

∆ y 4 ∆ y 1 = 0,196 0,012 = 16,3

∆ y 5 ∆ y 1 = 0,306 0,012 = 25,5

Pela arbitrariedade dos valores acima, não conseguimos determinar nenhum padrão de evolução, seja ela geométrico ou aritmético.

Resposta

  1. ∆ y 1 = 0,012   m ;
  2. ∆ y 2 = 0,049   m ;
  3. ∆ y 3 = 0,110   m ;
  4. ∆ y 4 = 0,196   m ;
  5. ∆ y 5 = 0,306   m .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Alan sai de Los Angeles, EUA, às 8 h dirigindo para San Francisco, distante 400m i . Ele viaja com uma velocidade constante de 50m p h . Beth sai de Los Angeles às 9 h e dirige constantemente a 60m p
Para visitar a avó, Julie dirige a primeira metade da distância a 40m p h , e a segunda, a 60m p h . Na viagem de volta, ela dirige a metade do tempo a 40m p h , e a outra metade do tempo a, 60m p h .
Um ciclista tem o gráfico da posição versus tempo mostrado na figura. Qual é a velocidade do ciclista em t =10s , t = 25s e t =35s ?
Para visitar a avó, Julie dirige a primeira metade da distância a 40m p h , e a segunda, a 60m p h . Na viagem de volta, ela dirige a metade do tempo a 40m p h , e a outra metade do tempo a, 60m p h .
Larry sai de casa às 9 h 05 m i n e vai correndo com velocidade constante até um poste de iluminação. Ele alcança o poste às 9 h 07 m i n , faz a volta imediatamente e corre para a árvore. Larry chega