No seu trabalho em um laboratório da polícia, é preciso projetar um aparato para medir as velocidades no cano das balas disparadas das armas. Sua solução é conectar um bloco de madeira de que se apoia sobre uma superfície horizontal a uma mola horizontal leve. A outra ponta da mola é presa a uma parede. Inicialmente, a mola está em seu comprimento de equilíbrio. Uma bala é disparada horizontalmente no bloco e permanece embutida nele. Depois que a bala atinge o bloco, este comprime a mola a uma distância máxima . Você mediu que o coeficiente de atrito cinético entre o bloco e a superfície horizontal é . A tabela a seguir lista algumas armas de fogo que você testará:

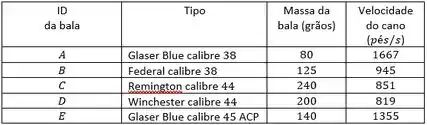
Um grão é uma unidade de massa igual a . Das balas de até , qual produzirá a máxima compressão da mola? E a mínima? Você deseja que a compressão máxima da mola seja . Qual deverá ser a constante de força da mola? Para a bala que produz a compressão mínima da mola, qual é a compressão se a mola tiver a constante de força calculada no item ?

Começando com o item .

Queremos saber qual bala produz a maior e a menor compressão na mola, para isso vamos observar a equação da energia, temos:

Como podemos ver a compressão da mola depende de , então quanto maior o momento maior será a compressão. Vamos calcular esse momento para cada e podemos usar as unidades da tabela.

Não esqueça que pela conservação de momento, por isso usamos os valores da tabela.

Vemos que o maior momento é o da bala , logo a maior compressão e o menor momento é o da bala , logo a menor compressão.

Vamos agora para o item .

Ele quer saber a constante de força da mola para que tenhamos uma compressão máxima de , então vamos usar a bala .

Para isso vamos usar a equação da energia, mas antes temos que saber o valor de , para isso vamos usar a conservação de momento, temos:

Usando as conversões do passo , temos:

Agora que temos o valor de , vamos atrás da constante da mola, temos:

Substituindo os valores que conhecemos, temos:

Assim temos que:

Agora o último item, o .

Agora ele quer que a gente calcule para bala que tem compressão mínima , com uma mola de constante igual a que achamos no item anterior.

Temos que saber antes a velocidade para essa bala, temos:

Usando as conversões do passo , temos:

Agora que temos essa velocidade vamos para a equação da energia, temos:

Substituindo os valores que conhecemos, temos:

Resolvendo essa equação de segundo grau temos que:

Com isso terminamos a nossa questão!