Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 6.Problemas Adicionais - Ex. 103
103- Uma corda pode suportar uma tração máxima de 40 N sem se partir. Uma criança amarra uma pedra de 0,37 kg em uma das extremidades da corda e, segurando a outra extremidade, faz a pedra girar em uma circunferência vertical de 0,91 m de raio, aumentando lentamente a velocidade até a corda arrebentar. (a) Em que ponto da trajetória está a pedra quando a corda arrebenta? (b) Qual é a velocidade da pedra quando a corda arrebenta?
Passo 1
A medida que a pedra vai girando as componentes de aceleração centrípeta e o peso vão se comportando da maneira como está na figura.
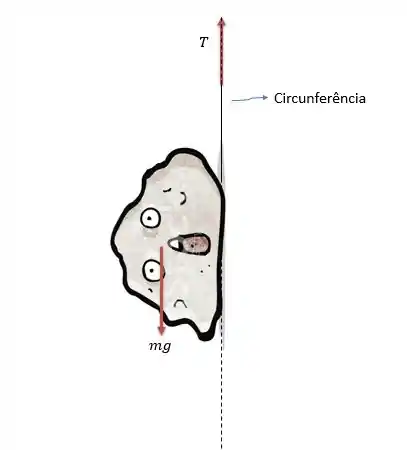
Porém temos também as forças de tração da corda e do peso da pedra.
O que deixa o sistema de forças na seguinte forma.
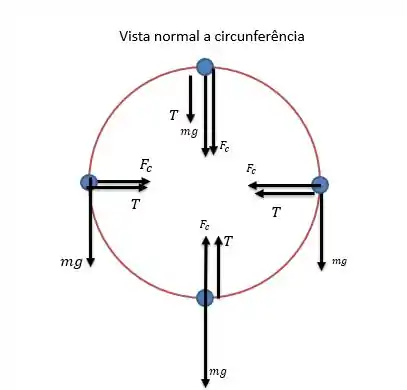
Onde é a força centrípeta que sempre aponta para o centro.
Passo 2
Fazendo a resultante das forças no ponto de cima da circunferência nós teremos:
O que nos dá uma força de tração igual a:
No ponto de baixo a força resultante será:
O que dá:
Que é uma força maior que no ponto de cima pois agora o peso contribui para a tração da corda.
No meio da circunferência vemos que a resultante na horizontal é:
Logo a máxima tração que a corda terá é o no ponto mais baixo do círculo, logo o limite da corda chegará primeiro no ponto mais baixo do círculo.
Passo 3
Utilizando a equação da tração no ponto mais baixo do círculo nós teremos a tração de e :
Substituindo e . Logo: