Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 34.Problemas Desafiadores - Ex. 116
116. A aberração esférica faz a imagem de um espelho esférico ficar borrada. Ela ocorre porque os raios paralelos que atingem o espelho em pontos afastados do eixo ótico são focalizados em pontos diferentes do foco produzido pelos raios paralelos paraxiais. Esse problema pode ser minimizado usando-se apenas a seção central do espelho esférico. Mostre que, para um espelho esférico côncavo, o foco se aproxima do vértice à medida que os
raios paralelos se afastam do eixo ótico. (Sugestão: deduza uma expressão analítica para a distância entre o vértice e o foco de um dado raio paralelo ao eixo ótico. Essa expressão deve depender do raio de curvatura do espelho e do ângulo de incidência compreendido entre a direção do raio incidente e a reta que une o centro do espelho com o ponto de incidência do raio.) Qual é o valor de que produz uma variação de na localização do
foco, em comparação com o foco formado quando é aproximadamente igual a zero?
Passo 1
Então galera para começarmos a resolver esse problema vamos montar um diagrama que representa essa situação, assim temos o seguinte:
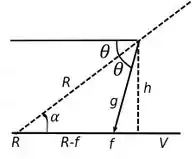
A parti desse diagrama vamos poder analisar o problema e resolver o item .
Para encontrar o que é pedido no item como temos porcentagem, podemos expressar isso da seguinte forma:
Onde temos como sendo e a distância focal para .
Passo 2
Agora vamos analisar nosso diagrama, para conseguirmos definir algo ou encontrar igualdades entre os parâmetros e assim encontrar a expressão analítica.
Primeiro vamos aplicar a lei dos senos para o triangulo maior que temos no nosso diagrama, assim temos:
Disso encontramos que:
Agora vamos fazer o seguinte, vamos dividir esse triangulo ao meio cortando ao meio, assim podemos fazer o seguinte, que
Mas como vimos mais acima que , assim temos que:
Com essa expressão podemos isolar , assim:
Pronto, encontramos a expressão analítica com o enunciado queria.
Passo 3
Agora vamos partir para o item , temos o seguinte:
Então temos que:
Agora se pegarmos a expressão que chegamos e definirmos que é a distância focal que encontramos para nessa expressão e fizermos , temos o seguinte:
Juntando tudo temos que:
Então temos que: