12.10. Quatro massas idênticas de 800 kg cada são colocadas nos cantos de um quadrado cujo lado mede 10,0 cm. Qual é a força gravitacional resultante (módulo, direção e sentido) sobre uma das massas em virtude das outras três?
Passo 1
Vamos começar desenhando a situação.
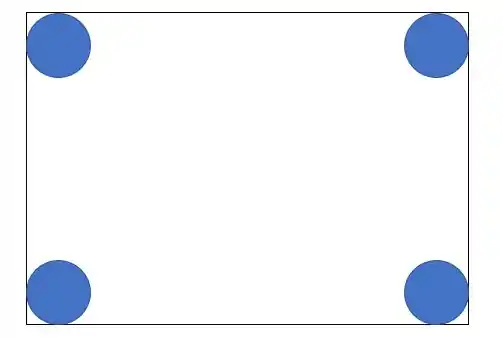
Vamos calcular a do canto superior esquerdo, então as forças estarão assim
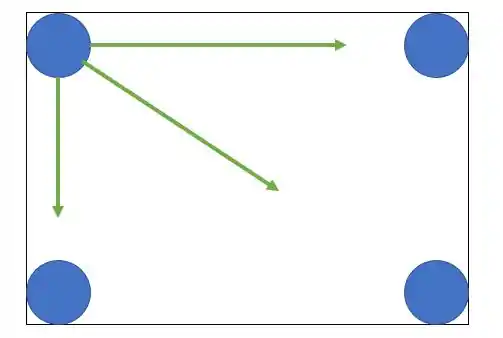
Vamos lembrar de como se calcular a força de atração gravitacional
Onde e são as massas, é a distância entre os centros de gravidade dos corpos e é a constante gravitacional universal
Passo 2
Agora a gente sabe que a distância entre a massa do canto superior direito e a massa do canto superior esquerdo é a mesma que a distância entre a massa do canto superior esquerdo e o canto inferior esquerdo, 10 centímetros, ou . Então a gente pode calcular essas forças de uma vez só.
Então a força é
Agora para a distância entre a massa do canto superior esquerdo e a do canto inferior direito, a gente precisa usar um Pitágoras
Então a força será
Passo 3
Beleza, então a gente tem isso
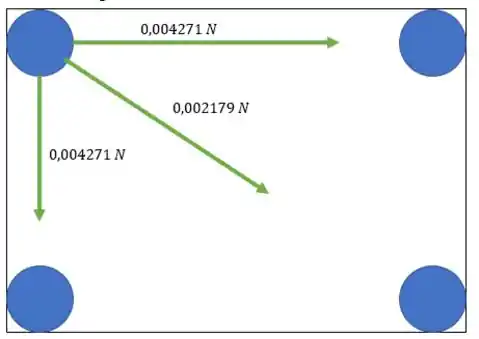
Mas a gente precisa calcular o módulo disso. Mas uma sacada aqui facilita as contas, o ângulo da força que age entre a massa superior esquerda e a inferior direta é , por que elas são extremos de um quadrado perfeito.
Então
Mas
Então para calcular o módulo temos
Logo
Módulo:
Direção: A diagonal que liga o canto superior esquerdo com o inferior direito
Sentido: 45° horário em relação ao eixo x
Pela simetria do problema, a gente consegue ver que todas as massas vão ter uma força resultante de mesmo módulo apontando para o centro do quadrado.
Resposta
Módulo:
Direção: A diagonal que liga o canto superior esquerdo com o inferior direito
Sentido: 45° horário em relação ao eixo x