Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 12.Exercício - Ex. 13
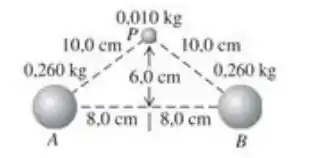
12.13. Duas esferas uniformes, cada uma com massa igual a 0,260 kg, estão fixas nos pontos A e B (Figura 12.33). Determine o módulo, a direção e o sentido da aceleração inicial de uma esfera uniforme com massa 0,010 kg quando ela é liberada do repouso no ponto P e sofrendo apenas atrações gravitacionais das esferas situadas em A e B.
Passo 1
Vamos começar desenhando a situação.
Vamos também lembrar de como se calcular a força de atração gravitacional
Onde e são as massas, é a distância entre os centros de gravidade dos corpos e é a constante gravitacional universal
Passo 2
Bem, a gente precisa calcular a aceleração da esfera pequena, e para isso a gente precisa da força, porque
Nós não podemos calcular a aceleração sem saber a força, mas a gente pode calcular a força com as informações que a gente já tem. Bem a força resultante vai ser a soma das forças de interação da esfera P com a esfera A e a esfera B, ou seja
Repare que as forças ficarão do seguinte modo
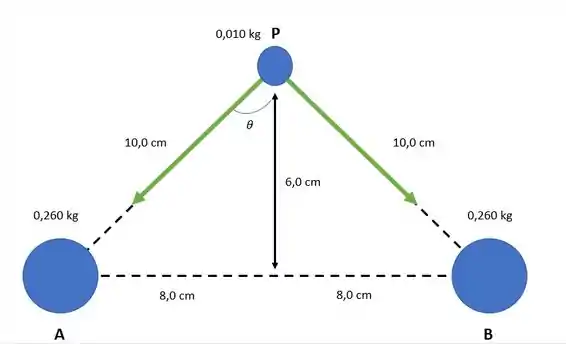
Então pela simetria do desenho, a gente só vai ter força na vertical da figura, as componentes na horizontal se cancelam. Sabendo disso a gente pode calcular a força vertical em uma das forças.
Logo
Agora vamos fazer para a outra força, mas olha só, repare no desenho que , e os ângulos também são iguais, logo e .
Então
Agora e .
E por tanto
Passo 3
Agora a gente já tem a força, então a gente já pode calcular a aceleração.
Olha só, a gente pode cortar o
Agora é só substituir os valores e calcular, lembrando de colocar tudo no SI, por tanto vira .
A gente já tem o módulo da aceleração. Agora vamos pensar sobre o sentido e a direção, olha só
Essa equação mostra que a força é um vetor que é o resultado de um escalar multiplicado pelo vetor aceleração, por tanto, a força e a aceleração tem mesma direção e sentido.
Logo a direção da aceleração é vertical e seu sentido é para baixo.
Resposta
Módulo:
Direção: Vertical
Sentido: Para baixo