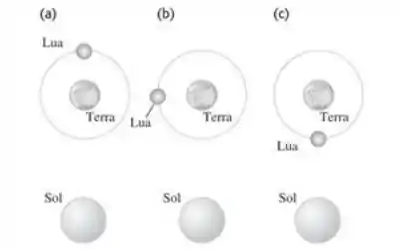
12.9. Determine o módulo, a direção e o sentido da força gravitacional resultante exercida pelo Sol e pela Terra sobre a Lua quando a Lua está em cada uma das posições indicadas na Figura 12.32 (Note que a figura não está desenhada em escala. Suponha que o Sol esteja no plano da órbita da Lua em torno da Terra, embora esse caso seja raro.) Use dados do Apêndice F.
Passo 1
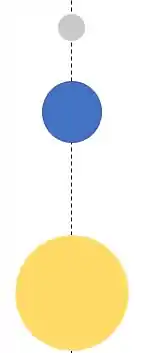
Vamos começar pelo item (a), os astros estão na seguinte disposição
Vamos lembrar de como se calcular a força de atração gravitacional
Onde e são as massas, é a distância entre os centros de gravidade dos corpos e é a constante gravitacional universal
Precisamos calcular as forças de interação entre a Terra e a Lua e a Terra e o Sol, somar vetorialmente e aí temos nossa força resultante. O interessante é o que o apêndice do livro nos dá a massa da Terra, a massa do Sol, a massa da Lua, a distância entre o a Terra e a Lua, a distância entre a Terra e o Sol e o raio da Terra, e isso é tudo que a gente precisa.
Vamos começar a resolver o primeiro item. Primeiro vamos calcular a força de interação entre a Terra e a Lua
E fazendo essa continha temos
E agora vamos fazer a força de interação entre o Sol e a Lua. O interessante aqui é perceber que a distância entre o Sol e Lua vai ser a distância entre o Sol e Terra somado com a distância entre a Lua e a Terra
Agora vamos fazer essa conta
Agora para ter a força total, a gente pode só somar direto as duas forças que calculamos, porque elas estão no mesmo sentido e direção.
Então a resposta do item (a) é
Módulo:
Direção: A linha que cruza os centros gravitacionais
Sentido: Em sentido ao Sol
Passo 2
Agora vamos para o segundo caso
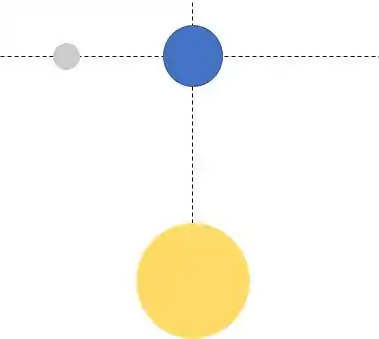
Olha só, a distância entre a Lua e a Terra permaneceu a mesma que no exercício anterior, então a gente não precisa calcular a força de novo 😊!
Agora, a distância entre o Sol e a Lua muda :/, e para descobrir a nova distância, a gente vai precisar de um pouco de Pitágoras.
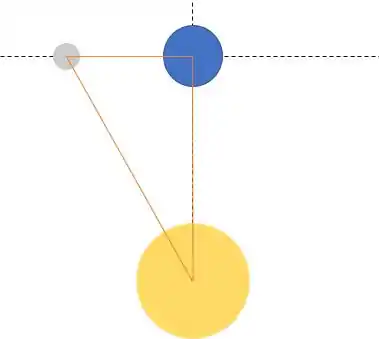
Temos esse triângulo, e a hipotenusa é a distância entre o Sol e a Lua, os catetos são as distâncias entre a Terra e a Lua e entre a Terra e o Sol. Vamos calcular
Olha só, podemos aproximar a distância entre a Lua e o Sol à distância entre a Terra e o Sol.
Agora vamos calcular essa força
Fazendo essa conta
Agora vamos somar vetorialmente.
Temos essas forças agindo na Lua
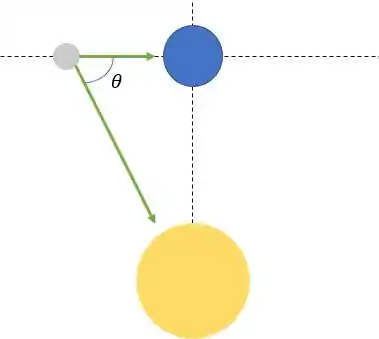
Agora a gente só precisa fazer a decomposição da força de interação entre o Sol e a Lua.
Vamos fazer isso
E agora vamos calcular para y
Então
Então para calcular o módulo
Já vamos calcular também a direção da força resultante, basta calcular
Logo
Então item (b) é
Módulo:
Direção: 89,85° a partir do eixo x
Sentido: Em sentido ao quarto quadrante
Passo 3
Agora finalmente vamos para o último item
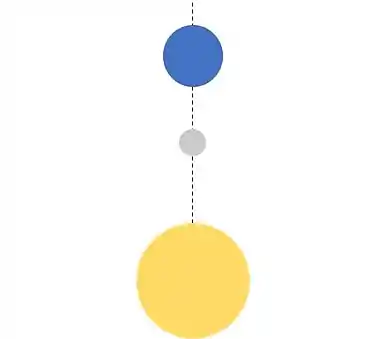
Bem, de novo a Lua continua à mesma distância da Terra, então não precisamos calcular 😊!
Agora vamos de novo ver a distância entre o Sol e a Lua, agora repare que essa distância é a mesma coisa que a distância entre o Sol e a Terra menos a distância entre a Terra e a Lua. Agora é só calcular.
Por tanto
Agora vamos fazer a soma. A gente vai estar na seguinte situação:
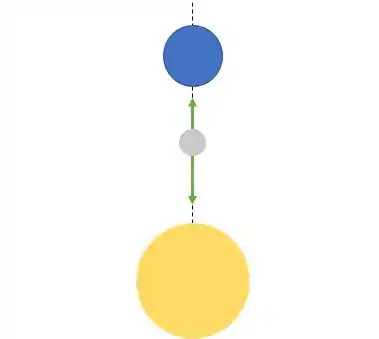
Vamos adotar para baixo como sentido positivo.
Então nossa força total fica
Módulo:
Direção: A linha que cruza os centros gravitacionais
Sentido: Em sentido ao Sol
Resposta
- Módulo:
- Módulo:
- Módulo:
Direção: A linha que cruza os centros gravitacionais
Sentido: Em sentido ao Sol
Direção: 89,85° a partir do eixo x
Sentido: Em sentido ao quarto quadrante
Direção: A linha que cruza os centros gravitacionais
Sentido: Em sentido ao Sol